自從“Attention is All You need”[1]這篇文章發佈之後,注意力機制開始廣為人知。雖然一開始注意力機制被應用於自然語言處理領域,但人們很快發現它也能夠用於處理圖像、點雲等數據結構,並且取得非常好的效果。
本文介紹如何用pytorch實現文章[1]提出的multi-head attention(MHA)。MHA是scaled dot-product attention(SDPA)[1,2]的改進。既然MHA是SDPA的multi-head版,那麼也許將SDPA稱為單頭注意力會比較形象。讓我們先從單頭注意力開始。
1 Scaled Dot-product Attention
SDPA的計算公式如下: \[ \text{Attention}(Q, K, V) = \text{Softmax}(\frac{QK^T}{\sqrt{d_k}})V \tag{1}\] 其中,\(Q\)、\(K\)和\(V\)分別為輸入的query、key和value向量。\(Q\)的尺寸為\(L\times E_q\),\(K\)的尺寸為\(S\times E_q\),\(V\)的尺寸為\(S\times E_v\)。
公式 1中,\(QK^T\)的計算可以理解為求query向量和key向量間的“匹配程度”,使得SDPA能夠根據匹配程度從value中取得相關的數據。Softmax函數在這裡起到歸一化的作用,使得SDPA的計算結果可以視為V的加權平均。
注意力機制是一個有趣的設計。RNN(Recurrent Neural Networks)結構面臨著長程記憶困難的問題;類似的,CNN(Convolutional Neural Networks)中也存在遠距離像素感知困難的問題。SDPA的特點是,為每一對query和key都作計算,而不考慮其時間或空間上的位置差距。
我個人的觀察是,注意力機制就好像構造了一個“完全二部圖”。這個二部圖由\(A\)和\(B\)兩個頂點集合組成,其中\(A\)集合代表query,\(B\)集合代表key和value。\(A\)和\(B\)之間的結點兩兩之間都有一條邊,邊的權重由query和key的“匹配程度”決定。類似SDPA,全連接層或卷積層也可以表示為二部圖,只不過其邊的權重是通過訓練得到的,固定的值,而在注意力機制中,邊的權重是動態的,根據query和key計算得到的。
1.1 Attention的縮放係數
從公式 1可以看到,在執行Softmax函數前,SDPA使用係數\(\frac{1}{\sqrt{d_k}}\)對輸入作了縮放。為什麼是\(\sqrt{d_k}\),而不是其它係數呢?本節主要摘錄蘇劍林的系列文章中的結論,對這個問題作簡要的討論。
Softmax是一個將向量映射為向量的函數。首先,我們注意到Softmax輸入向量的方差對於其輸出向量的分佈有重要影響。
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
np.random.seed(0)
length = 32
samples = []
n_samples = 32
for i in range(n_samples):
m = i / n_samples * 10
x = np.random.randn(length) * m
y = np.array(torch.softmax(torch.tensor(x), dim=0))
samples.append((sorted(y), np.var(x)))
samples.sort(key=lambda x: x[1]) # 按方差排序
fig = plt.figure()
ax = plt.gca()
cax = ax.matshow(np.array([s for s, i in samples]).transpose())
ax.set_xticklabels([f'{i:.2f}' for s, i in samples])
fig.colorbar(cax);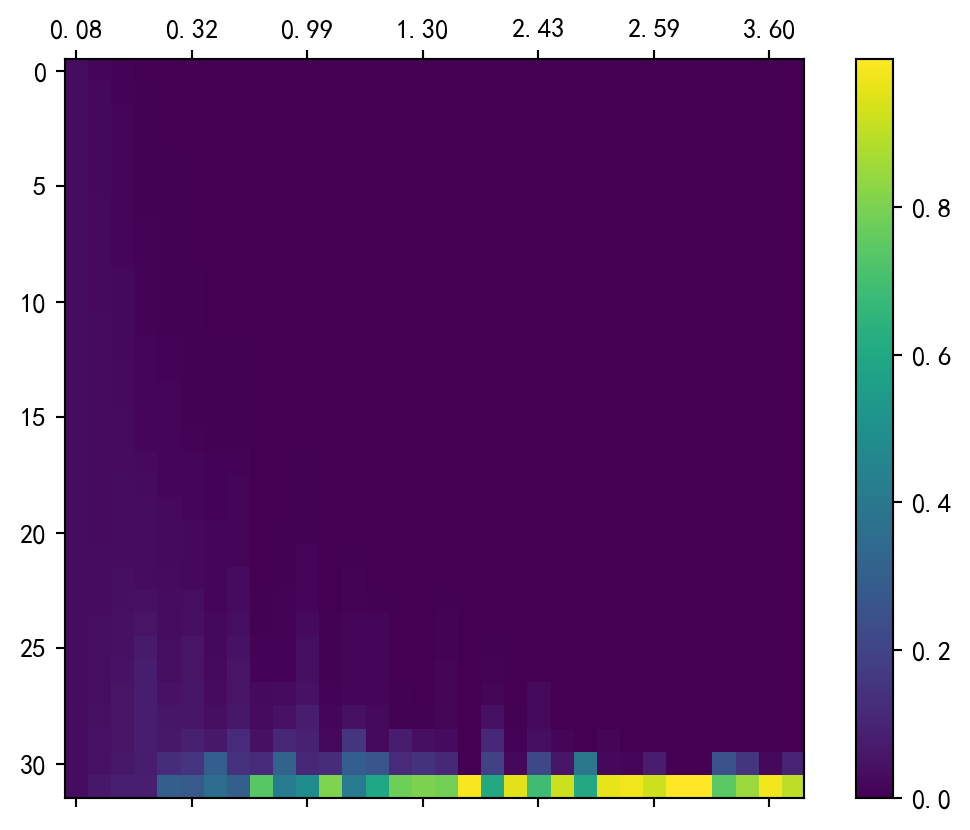
由圖 1可見,Softmax函數的輸入向量方差越小,則輸出越接近\(\vec 0\);反之,Softmax的輸出越接近one-hot編碼,即只有一個元素是1,其它元素都接近0. 然而,這兩種極端情況都容易引發梯度消失問題。(這在我的《Softmax函數的性質》一文中已經給出了推導。)
為了避免梯度消失,我們既不希望Softmax的輸出接近\(\vec 0\),也不希望其成為one-hot編碼。下面的程序通過直觀的方式演示了其中的原因:
# 向量的長度
length = 128
# 縮放係數,影響輸入向量的方差大小
scales = [2**(i / 3) for i in range(10)]
xs = []
ys = []
for _ in range(1000):
# 隨機選擇一個縮放係數
m = np.random.choice(scales)
# 隨機初始化Softmax的輸入,並縮放
x = torch.tensor(np.random.randn(length) * m, requires_grad=True)
# 執行Softmax函數
y = torch.softmax(x, dim=0)
# 橫軸為max(y)
xs.append(y.max().item())
label = torch.rand(y.shape)
loss = torch.abs(label - y).mean()
loss.backward()
# 縱軸為梯度絕對值的最大值
ys.append(x.grad.abs().max().item())
plt.scatter(xs, ys)
plt.xlabel('Softmax輸出的最大值')
plt.ylabel('梯度絕對值的最大值')
plt.show()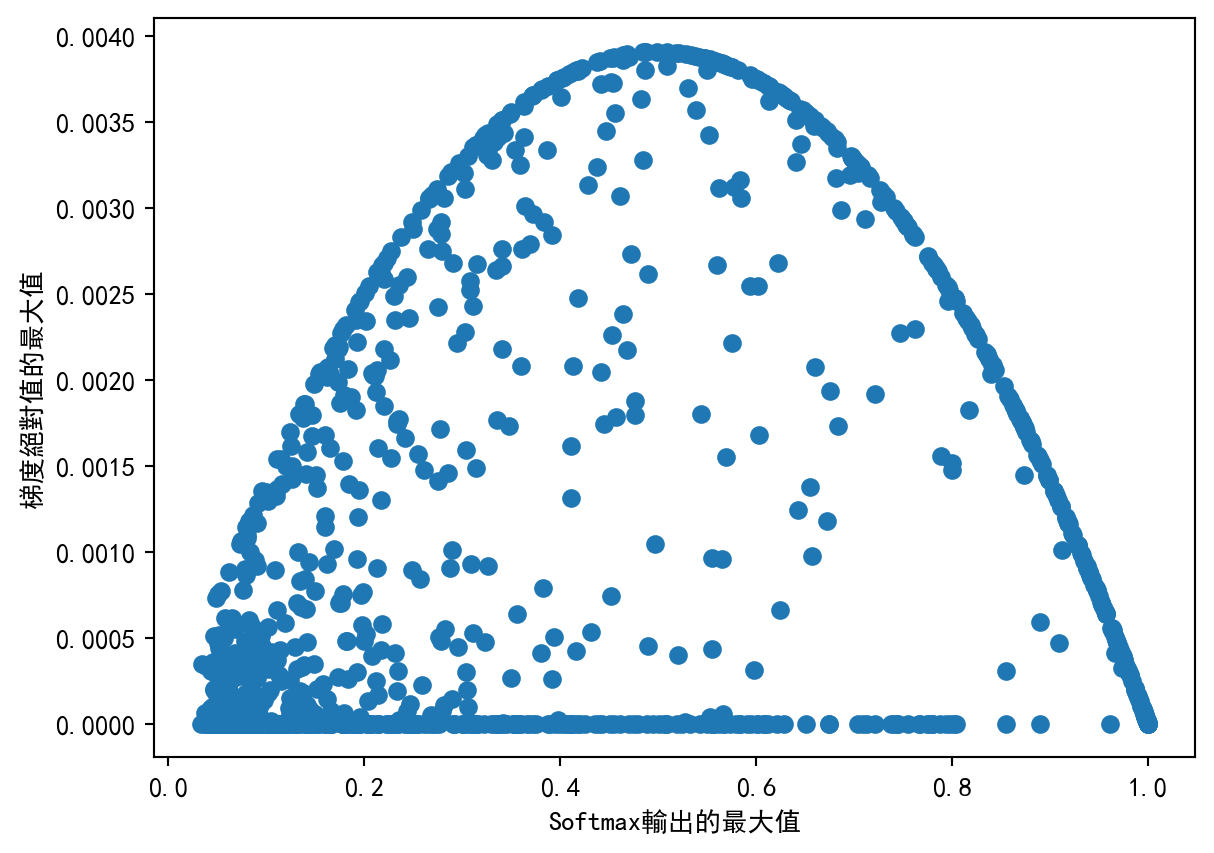
從圖 2可以看到,當Softmax的輸入接近\(0\)向量或者one-hot向量的時候,容易發生梯度消失現象,此時梯度的絕對值接近\(0\).
綜上所述,為盡量避免Softmax的梯度消失,控制輸入向量的方差很重要。假設\(\vec q\)和\(\vec k\)都是\(0\)均值的,二者相互獨立,方差分別為\(v_q\)和\(v_k\),不難證明它們的內積\(\vec q^T \vec k\)的數學期望為\(0\)。展開證明
\[ \begin{align*} \mathbb{E}(\vec q^T \vec k) &= \mathbb{E}\left(\sum_i q_i k_i\right) \\ &= \sum_i \mathbb{E}(q_i k_i) \\ &= \sum_i \mathbb{E}(q_i) \mathbb{E}(k_i) \\ &= \sum_i 0 \cdot 0 \\ &= 0. \end{align*} \]展開證明
\[ \begin{align*} \text{Var}(\vec q^T \vec k) &= \text{Var}\left(\sum_{i=1}^{d_k} (q_i k_i)\right) \\ \end{align*} \] 假設\(\vec q^T \vec k\)的任意兩個維度都是獨立同分佈的,那麼 \[ \begin{align*} \\ \text{Var}(\vec q^T \vec k) &= d_k Var(q_i k_i) \\ &= d_k (\mathbb E(q_i^2 k_i^2) - (\mathbb E(q_i k_i))^2)\\ &= d_k (\mathbb E(q_i^2)\mathbb E(k_i^2) - (\mathbb E(q_i) \mathbb E(k_i))^2)\\ &= d_k (\mathbb E(q_i^2)\mathbb E(k_i^2) )\\ &= d_k \left( Var(q_i) Var(k_i) \right) \\ &= d_k v_q v_k \end{align*} \] 於是\({\rm Var} (\vec q^T \vec k/\sqrt{d_k})=v_q v_k\)。因此,假設輸入的query和value是標準正態分佈(均值為\(0\),方差為\(1\)),那麼經過\(1/\sqrt{d_k}\)的縮放處理,就能保持softmax的輸入也是標準正態分佈,避免方差過小或過大。
1.2 代碼實現
在充分理解清楚SDPA的計算公式的前提下,用pytorch實現它就不困難。需要注意的是公式 1中沒有體現attention mask,但我們要在代碼實現中支持它。attention mask用於在訓練中阻止模型到未來的token,這對訓練聊天機器人、機器翻譯模型是等生成式模型是必要的。
在實現中,mask矩陣的值會被加到注意力矩陣上。如果mask矩陣中有一個值非常小(接近\(-\infty\)),那麼對應的注意力就會在softmax中被抑制。
下列代碼實現了scaled dot-product attention:
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
def my_scaled_dot_product_attention(q, k, v, mask=None):
embed_dim = q.shape[-1]
attn_weights = torch.einsum('nle,nse->nls', q, k)
attn_weights /= np.sqrt(embed_dim)
if mask is not None: attn_weights += mask
attn_weights = torch.softmax(attn_weights, dim=-1)
ret = torch.einsum('nls,nse->nle', attn_weights, v)
return ret, attn_weights讓我們看看實現的my_scaled_dot_product_attention函數能不能正常運行:
batch_size = 1
length = 2
embed_dim = 4
q = torch.rand((batch_size, length, embed_dim))
k = torch.rand((batch_size, length, embed_dim))
v = torch.rand((batch_size, length, embed_dim))
mask = torch.rand((length, length))
ret, attn_weights = my_scaled_dot_product_attention(q, k, v, mask)
print('attention操作返回結果:', ret)
print('attention矩陣為:', attn_weights)attention操作返回結果: tensor([[[0.5092, 0.4412, 0.1042, 0.1914],
[0.6837, 0.5136, 0.1024, 0.2412]]])
attention矩陣為: tensor([[[0.5479, 0.4521],
[0.3397, 0.6603]]])一個檢查實現正確性的小技巧是,觀察返回attention矩陣的各列之和是否為1. 如果不為1,說明實現有問題。
print(attn_weights.sum(-1))
assert torch.all(attn_weights.sum(-1) - 1 < 1e-6)tensor([[1., 1.]])在準備好scaled dot product attention的基礎上,我們便可以著手實現multi-head attention了。
2 Multi-head Attention
根據原論文描述,MHA的實現為: \[\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O \] 其中\(\text{head}_i = \text{Attention}(QW^Q_i , KW^K_i ,VW^V_i)\). 據此可知,MHA操作為:
- 將query、key和value拆分成若干個head,對這些head分別作線性變換;
- 對每個head分別執行scaled dot-product attention;
- 將所有head的attention的結果合併,經過一層線性變換後返回。
通過在多個head上執行attention,MHA允許模型在不同的子空間收集不同位置的信息,增加了attention機制的表達能力。
代碼實現如下:
class MyMultiheadAttention(nn.Module):
def __init__(
self,
embed_dim,
num_heads,
):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.in_proj_weight = nn.Parameter(
torch.rand((3 * embed_dim, embed_dim))
)
self.in_proj_bias = nn.Parameter(
torch.rand((3 * embed_dim))
)
self.out_proj = nn.Linear(embed_dim, embed_dim)
def forward(self, query, key, value, attn_mask=None):
L, N, q_dim = query.shape
S, N, k_dim = key.shape
S, N, v_dim = value.shape
assert self.embed_dim % self.num_heads == 0
weight_query, weight_key, weight_value = self.in_proj_weight.chunk(3)
bias_query, bias_key, bias_value = self.in_proj_bias.chunk(3)
query = F.linear(query, weight_query, bias_query)
key = F.linear(key, weight_key, bias_key)
value = F.linear(value, weight_value, bias_value)
# L, N, E -> N*n_heads, L, E/n_heads
query = query.view(L, N * self.num_heads, -1).permute(1, 0, 2)
key = key.view(S, N * self.num_heads, -1).permute(1, 0, 2)
value = value.view(S, N * self.num_heads, -1).permute(1, 0, 2)
out, attn_weights = my_scaled_dot_product_attention(query, key, value, mask=attn_mask)
out = out.permute(1, 0, 2).reshape(L, N, -1)
attn_weights = attn_weights.reshape(N, -1, L, S).mean(1)
out = self.out_proj(out)
return out, attn_weights首先,我們先比較一下本文實現的multi-head attention和torch官方的實現的參數設置。我們將會看到所有參數名稱和參數尺寸都是一致的。這表明我們的multi-head attention與torch的官方實現兼容。
batch_size = 2
embed_dim = 16
num_heads = 4
torch_mha = nn.MultiheadAttention(embed_dim, num_heads)
for n, p in torch_mha.named_parameters():
print(n, p.shape)
print('')
my_mha = MyMultiheadAttention(embed_dim, num_heads)
for n, p in my_mha.named_parameters():
print(n, p.shape)in_proj_weight torch.Size([48, 16])
in_proj_bias torch.Size([48])
out_proj.weight torch.Size([16, 16])
out_proj.bias torch.Size([16])
in_proj_weight torch.Size([48, 16])
in_proj_bias torch.Size([48])
out_proj.weight torch.Size([16, 16])
out_proj.bias torch.Size([16])接下來,我們檢查我們實現的MHA和torch版本MHA的輸出是否完全一致。在進行比較之前,我們先進行參數的複製,保持兩個模塊的參數完全相同。
my_mha_parameters = dict(my_mha.named_parameters())
for n, p in torch_mha.named_parameters():
my_mha_parameters[n].data.copy_(p)
assert torch.all(p == my_mha_parameters[n])下列代碼對函數的輸出進行檢查:
query = torch.rand((length, batch_size, embed_dim))
key = torch.rand((length, batch_size, embed_dim))
value = torch.rand((length, batch_size, embed_dim))
# prepare mask
attn_bias = torch.zeros(length, length, dtype=query.dtype)
temp_mask = torch.ones(length, length, dtype=torch.bool).tril(diagonal=0)
attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
attn_bias.to(query.dtype)
ret, attn_weights = my_mha(query, key, value, attn_mask=attn_bias)
ret2, attn_weights2 = torch_mha(query, key, value, need_weights=True, attn_mask=attn_bias)
error = torch.mean(torch.abs(ret - ret2)).item()
error2 = torch.mean(torch.abs(attn_weights - attn_weights2)).item()
print(f'Difference: {error:.4f}, {error2:.4f}')
assert error < 1e-6 and error2 < 1e-6Difference: 0.0000, 0.0000檢查結果表明我們實現的multi-head attention輸出與torch官方實現的完全一致,驗證了代碼的正確性。
3 練習題
例子 1 改變MHA的heads數會如何改變MHA的參數量?
參考答案
MHA的參數量與head的數量無關,這從代碼中也能很容易看出來。
實驗也驗證了這一點。
embed_dim = 16
num_heads = 4
mha1 = nn.MultiheadAttention(embed_dim, num_heads)
mha2 = nn.MultiheadAttention(embed_dim, num_heads * 2)
def count_parameters(m):
c = 0
for p in m.parameters(): c += p.numel()
return c
print(count_parameters(mha1), count_parameters(mha2))1088 1088例子 2 在自注意力機制中,MHA的時間複雜度是多少?和head數有關嗎?
參考答案
首先,由公式 1可以看出,單頭注意力機制的時間複雜度是\(O(n^2d)\),其中\(n\)為序列長度,\(d\)為特征維度。
接下來考慮MHA的時間複雜度。MHA先對輸入向量作線性變換得到Q、K、V,這部分的時間複雜度為\(O(nd^2)\);然後這些特征被拆分為\(n\)個head,分別做attention,這個部分的時間複雜度為\(O(n^2\frac{d}{h} * h)\),其中\(h\)為head數。最後MHA再做一次線性變化,時間複雜度為\(O(nd^2)\).
因此,總的來看,MHA的時間複雜度為\(O(n^2d + nd^2)\),與head數無關。
從stack overflow的這個網頁可以看到一些有趣的討論:https://stackoverflow.com/questions/65703260/computational-complexity-of-self-attention-in-the-transformer-model4 總結
推薦閱讀:
- torch官方的scaled dot-product attention文檔中簡要介紹了一種scaled dot-product attention的python實現方式。
- 論文MQA[3]中的Background一節對各類Attention有詳細介紹,推薦一讀。