之前有一段時間,我需要復習梯度下降和反向傳播來應付面試。 雖然梯度下降和反向傳播都屬於基礎,但要想順暢地在有限時間内把它寫出來,還是挺不容易,必須要提前準備才行。本文記錄了筆者的復習成果。
在編寫代碼的過程中,尤其要注意數組尺寸的正確性。计算和编写代码的过程中,犯錯常有的。最好能通過梯度檢查來校驗梯度計算的正確性,這樣我們才有信心根據計算得到的梯度進行梯度下降。
本文代碼以示範為目的,並不適用於工程實踐,因此文中的程序不會追求擴展性、運行效率等,而是盡量簡潔明瞭。
本文嘗試通過numpy庫實現梯度下降,不依賴任何深度學習工具。我們先import numpy.
import numpy as np
np.random.seed(0)1 多層感知機的前向計算
本節將實現一個多層感知機,用它來回歸sin函數。
為簡便起見,這個多層感知機只使用relu激活函數。
1.1 建立模型
def relu(x):
return np.clip(x, 0, None)以下代碼定義了MLPRegression類的初始化函數。我們通過硬編碼的方式將這個多層感知機設置為3層,并規定每層的輸入輸出維度。
class MLPRegression:
def __init__(
self,
):
self.w1 = np.random.randn(1, 16)
self.b1 = np.random.randn(16, 1)
self.w2 = np.random.randn(16, 32)
self.b2 = np.random.randn(32, 1)
self.w3 = np.random.randn(32, 1)
self.b3 = np.random.randn(1, 1)在前向傳播階段,這個多層感知機在每一層綫性層后應用了一個relu激活函數。最後一層是例外的,沒有任何激活函數,這樣就不會限制模型擬合函數的值域。
與一般的torch代碼不同,我們在forward過程中需要手動保存cache變量,記錄模型的中間執行結果。在反向傳播過程中,我們需要使用它們來計算梯度。
def mlp_regression_forward(self, x, y=None):
d_in, bs = x.shape
h1 = self.w1.transpose() @ x + self.b1 # d_1, bs
a1 = relu(h1)
h2 = self.w2.transpose() @ a1 + self.b2 # d_2, bs
a2 = relu(h2)
h3 = self.w3.transpose() @ a2 + self.b3 # 1, bs
cache = {
'x': x,
'h1': h1,
'a1': a1,
'h2': h2,
'a2': a2,
'h3': h3,
'y': y
}
if y is not None:
loss = np.mean(np.abs(y - h3))
else:
loss = None
return h3, loss, cache
MLPRegression.forward = mlp_regression_forward接下來我們試運行一下forward函數。函數返回pred,loss,cache三個變量,分別對應模型的預測值,損失以及用於計算梯度的中間變量。
r = MLPRegression()
pred, loss, cache = r.forward(np.random.random((1, 2)))
for k, v in cache.items():
print(k, v.shape if v is not None else 'None')x (1, 2)
h1 (16, 2)
a1 (16, 2)
h2 (32, 2)
a2 (32, 2)
h3 (1, 2)
y None2 多層感知機的反向傳播
反向傳播代碼是本文的重點。在編寫反向傳播代碼之前,我們先復習幾個重要函數的梯度計算。
2.1 MAE函數的梯度
代碼中,我們使用的損失函數為MAE,即 \[ l=\frac{1}{m} \sum_i^m |\hat y - y| \] 易知其導數為 \[ \frac{\mathrm d l}{\mathrm d \hat y} = \left\{ \begin{aligned} 1&, \hat y > y \\ -1&, \hat y < y \end{aligned} \right. \] 姑且不考慮0點処該函數沒有導數的問題。
2.2 ReLU函數的梯度
ReLU函數的公式為: \[ a=\text{ReLU}(h)=\max(0, h) \] 易得其導數(同樣不考慮\(h=0\) 時沒有導數的問題)為 \[ \frac{\mathrm d a}{\mathrm dh} = \left\{ \begin{aligned} 1 & ,h > 0 \\ 0 & ,h < 0 \end{aligned} \right. \]
2.3 綫性層的梯度
設MLP的一層綫性變換為 \[ \vec y=\mathbf W^T \vec x + \vec b, \] 其中\(\vec b\in \mathbb R^{d_\text{out}}, \vec x\in \mathbb R^{d_\text{in}, 1}\) , 應用鏈式法則,可以求得以下梯度: \[\begin{aligned} \frac{\partial l}{\partial \mathbf W} &= \vec x \left(\frac{\partial l}{\partial \vec y}\right)^T\\ \frac{\partial l}{\partial \vec b} &= \frac{\partial l}{\partial \vec y}\\ \frac{\partial l}{\partial \vec x} &= \mathbf W \left(\frac{\partial l}{\partial \vec y}\right) \\ \end{aligned}, \] 其中\(l\)為模型的損失。
2.4 反向傳播代碼
根據以上推導,可以寫出如下的反向傳播代碼。該函數返回一個dict用於存儲各個變量的梯度。
def mlp_regression_backward(self, cache):
y = cache['y']
_, bs = y.shape
pred = cache['h3']
dh3 = 1. / bs * (
np.int64(pred > y)
- np.int64(pred < y)
) # 1, m
# w3.T @ a2 + b3 = h3
dw3 = cache['a2'] @ dh3.T # d_2, 1
db3 = dh3.sum(axis=-1, keepdims=True) # 1, 1
da2 = self.w3 @ dh3 # d_2, bs
# a2 = relu(h2)
dh2 = da2 * (cache['h2'] > 0) # d_2, bs
# h2 = w2.T @ a1 + b2
dw2 = cache['a1'] @ dh2.T # d_1, d_2
db2 = dh2.sum(-1, keepdims=True) # d_2, 1
da1 = self.w2 @ dh2 # d_1, bs
# a1 = relu(h1)
dh1 = da1 * (cache['h1'] > 0) # d_1, bs
# h1 = w1.T @ x + b1
dw1 = cache['x'] @ dh1.T # d_in, d_1
db1 = dh1.sum(-1, keepdims=True) # d_in, 1
return {
'dw3': dw3, 'db3': db3,
'dw2': dw2, 'db2': db2,
'dw1': dw1, 'db1': db1
}
MLPRegression.backward = mlp_regression_backward
r = MLPRegression()
yh, loss, cache = r.forward(
np.array([1, 2]).reshape(1, 2),
y=np.array([2, 3]).reshape(1, 2),
)
grads = r.backward(cache)
for k, v in grads.items():
print(k, v.shape)dw3 (32, 1)
db3 (1, 1)
dw2 (16, 32)
db2 (32, 1)
dw1 (1, 16)
db1 (16, 1)2.5 梯度检查
一次性正確寫完梯度反傳并不容易。梯度檢查是校驗梯度計算正確性的重要方法。 根據梯度的定義,設損失函數為\(J\) ,那麽梯度可以用如下方法估計: \[
\frac{\partial J(x;\vec \theta)}{\partial \theta_i} \approx \frac{J(x;[\theta_1, \theta_2, \cdots, \theta_i + \epsilon, \cdots, \theta_n]) - J(x;[\theta_1, \theta_2, \cdots, \theta_i - \epsilon, \cdots, \theta_n] )}{2\epsilon}
\] 下面提供的parameters_to_vector,restore_parameters_from_vector函數實現了將模型參數轉化爲向量和從向量恢復模型參數的功能。grads_to_vector和vector_to_grads也起類似作用。基於此我們可以實現梯度檢查。
def parameters_to_vector(self):
ret = [self.w1, self.b1, self.w2, self.b2, self.w3, self.b3]
ret = [it.reshape((-1,)) for it in ret]
return np.concatenate(ret)
MLPRegression.parameters_to_vector = parameters_to_vector
def grads_to_vector(self, grads):
ret = [grads[k] for k in ['dw1', 'db1', 'dw2', 'db2', 'dw3', 'db3']]
ret = [it.reshape((-1,)) for it in ret]
return np.concatenate(ret)
MLPRegression.grads_to_vector = grads_to_vector
def vector_to_grads(self, vec):
params = [self.w1, self.b1, self.w2, self.b2, self.w3, self.b3]
names = ['dw1', 'db1', 'dw2', 'db2', 'dw3', 'db3']
param_sizes = [it.size for it in params]
param_offsets = [0] + param_sizes
for i in range(len(param_offsets) - 1):
param_offsets[i + 1] += param_offsets[i]
grads = [vec[param_offsets[i]:param_offsets[i + 1]].reshape(p.shape) for i, p in enumerate(params)]
return {k: v for k, v in zip(names, grads)}
MLPRegression.vector_to_grads = vector_to_grads
def restore_parameters_from_vector(self, vec):
params = [self.w1, self.b1, self.w2, self.b2, self.w3, self.b3]
param_sizes = [it.size for it in params]
param_offsets = [0] + param_sizes
for i in range(len(param_offsets) - 1):
param_offsets[i + 1] += param_offsets[i]
params2 = [vec[param_offsets[i]:param_offsets[i + 1]].reshape(p.shape) for i, p in enumerate(params)]
w1, b1, w2, b2, w3, b3 = params2
self.w1 = w1
self.b1 = b1
self.w2 = w2
self.b2 = b2
self.w3 = w3
self.b3 = b3
MLPRegression.restore_parameters_from_vector = restore_parameters_from_vector
r = MLPRegression()
x = np.random.randn(1, 2)
y = np.random.randn(1, 2)
yh, loss, cache = r.forward(x, y)
grads = r.backward(cache)
grads_vec = r.grads_to_vector(grads)
grads_est = grads_vec * 0
parameters_vec = r.parameters_to_vector()
print(grads_vec.shape)
num_parameters = len(grads_vec)
eps = 1e-4
for i in range(num_parameters):
parameters_vec_copy = parameters_vec.copy()
parameters_vec_copy[i] += eps
r.restore_parameters_from_vector(parameters_vec_copy)
_, loss, _ = r.forward(x, y)
parameters_vec_copy = parameters_vec.copy()
parameters_vec_copy[i] -= eps
r.restore_parameters_from_vector(parameters_vec_copy)
_, loss2, _ = r.forward(x, y)
grad = (loss - loss2) / (2 * eps)
grads_est[i] = grad
difference = np.max(np.abs(grads_vec - grads_est))
print('Diff:', difference)(609,)
Diff: 3.414629690112747e-11由代碼輸出可見,文章給出的梯度計算方法與梯度估算法的結果相差無幾,這證明了本文推導的正確性。
3 训练
以下程序以最基礎的SGD方法訓練了給出的模型,並打印損失函數。
import tqdm.notebook as tqdm
learning_rate = 1e-3
r = MLPRegression()
total_iters = 10000
pbar = tqdm.tqdm(total=total_iters)
loss_records = []
for i in range(total_iters):
x = np.random.rand(1, 16) * 10 - 5
y = np.sin(x)
yh, loss, cache = r.forward(x, y)
grads = r.backward(cache)
for k, v in grads.items():
assert k.startswith('d')
param_name = k[1:]
param = getattr(r, param_name)
assert param.shape == v.shape, (param.shape, v.shape)
setattr(r, param_name, param - v * learning_rate)
if i % 10 == 0:
loss_records.append((i, loss))
pbar.set_description(f'loss: {loss:.4f}')
pbar.update()import matplotlib.pyplot as plt
loss_records = np.array(loss_records)
plt.plot(loss_records[:, 0], loss_records[:, 1])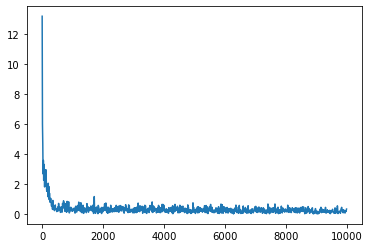
訓練完成後,模型的推理效果如圖所示。由圖可見,模型成功擬合了 函數。
這裏模型的擬合效果并不完美。畢竟這只是一個三層的小型MLP,它還是有很大改進空間的。
x = np.linspace(-5, 5, 1000)[None, :]
y, _, _ = r.forward(x)
plt.figure()
x = x.reshape((-1,))
y = y.reshape((-1,))
plt.plot(x, np.sin(x))
plt.plot(x, y)
plt.legend([
'sin(x)',
'pred'
])
plt.show()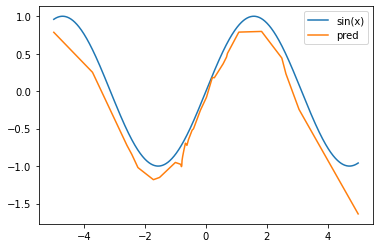
4 附录
附錄提供了正文未使用到的一些常用函數的梯度推導。這些推導對實現分類器會有幫助,但本文就不給出詳細實現了。
4.1 Sigmoid的梯度推導
設\(\sigma(x)=\frac{1}{1+e^{-x}}\)是sigmoid函數。那麼\(\sigma(x)\) 的導數爲 \[\begin{aligned} \sigma'(x) &= \frac{e^{-x}}{(1 + e^{-x})^2} \\ &= \frac{1}{1 + e^{-x}} \frac{e^{-x}}{1+e^{-x}} \\ &= \sigma(x)(1-\sigma(x)) \end{aligned} \]
4.2 二值交叉熵函數的梯度推導
假設模型的最後一層激活函數為sigmoid函數,即\(\vec a = \sigma(\vec h)\). 損失函數為: \[ J(\vec a)=-\frac{1}{m} \sum_i^m \left( y_i \log (a_i) + (1-y_i)\log(1 - a_i) \right) \] 於是 \[ \frac{\partial J}{\partial a_i} = -\frac{1}{m} \left( y_i \frac{1}{a_i} -(1 - y_i)\frac{1}{1-a_i} \right) \] \[ \begin{aligned} \therefore \frac{\partial J}{\partial h_i} = \frac{\partial J}{\partial a_i} \frac{\partial a_i}{\partial h_i} & = -\frac{1}{m} \left( y_i \frac{1}{a_i} -(1 - y_i)\frac{1}{1-a_i} \right) (a_i)(1 - a_i) \\ &= -\frac{1}{m} \left(y_i(1-a_i) - (1 - y_i)a_i \right)\\ &= -\frac{1}{m} \left(y_i - y_ia_i - a_i + y_ia_i\right) \\ &= \frac{1}{m} (a_i - y_i) \end{aligned} \] \[ \therefore \frac{\partial J}{\partial \vec h} = \frac{1}{m}(\mathbf A - \mathbf Y) \] 假设\(\mathbf A\) 是由特征\(\vec x\)经过一层线性层,再經過softmax激活函数得来的,即 \[ \mathbf A=\sigma(\vec h) = \sigma( \vec w^T\mathbf X+ \vec b), \] 那麽 \[ \begin{aligned} \therefore \frac{\partial J}{\partial \vec w} &= \frac{1}{m}\mathbf X(\mathbf A- \mathbf Y)^T \\ \frac{\partial J}{\partial \vec b} &= \frac{1}{m}(\mathbf A - \mathbf Y) \end{aligned} \]