\[ \def \vec#1{{\boldsymbol{#1}}} \def \mat#1{{\mathbf{#1}}} \def \argmax#1{\underset{#1}{\operatorname{argmax}}} \def \argmin#1{\underset{#1}{\operatorname{argmin}}} \]
<script>
MathJax = {
tex: {
tags: 'ams' // should be 'ams', 'none', or 'all'
}
};
</script>\[ \def \vx{{\vec x}} \def \vy{{\vec y}} \def \vtheta{{\vec \theta}} \def \vmu{{\vec \mu}} \def \vsigma{{\vec \sigma}} \def \vepsilon{{\vec \epsilon}} \def \vtau{{\vec \tau}} \def \mI{{\mat I}} \def \mZero{{\mat 0}} \def \mSigma{{\mat \Sigma}} \def \E{{\mathbb E}} \def \N{{\mathcal N}} \def \KL{{D_\text{KL}}} \]
前言
想寫篇文章回顧兩篇重要工作。一個是DDPM[1],另一個是DDIM[2].
DDPM[1]展現了擴散模型的強大生成能力,圖像質量可與當時主流GAN媲美。它逐步將圖像轉化為噪聲,再訓練神經網絡學習逆向去噪過程。
DDPM原本需要上千步迭代生成圖像,效率低。後續提出的DDIM[2]證明了推理步數可以壓縮,提升了實用性。
本文會梳理從DDPM到DDIM的關鍵推導過程,統一兩篇文章的數學符號,讓推理過程更加清晰容易理解。
講故事的順序是:
- 先介紹樣本的前向過程,說明樣本是如何擴散變成噪聲的。
- 然後介紹反向過程,說明模型是如何去噪的。
- 接著說明根據反向過程,如何推導出擴散模型的優化目標。
- 最後,演示如何用代碼訓練出一個去噪模型,並且展示如何用這個模型採樣。
我會對DDPM和DDIM分別重複上面這個流程。
DDPM
首先看一下DDPM。設初始圖像為\(\vx_0\),擴散模型會在每一步\(t=1,2,3,4,\dots,T\)添加噪聲,將\(\vx_{t-1}\)變成\(\vx_t\),最終得到\(\vx_T\). 這個逐步加噪聲的過程叫作前向過程。
根據這個定義,前向過程是馬爾科夫過程,即\(q(\vx_t|\vx_0, \vx_1, \dots, \vx_{t-1}) = q(\vx_t|\vx_{t-1})\).
在本文中,我會用Python代碼做一些簡單的演示和實驗。下面的代碼將T設為1000.
import torch
import numpy as np
T = 1000 前向過程
DDPM規定了前向過程的具體形式: \[ q(\vx_t|\vx_{t-1}):=\N (\vx_{t}; \sqrt{1 - \beta_t}\vx_{t-1}, \beta_t \mI) \tag{1}\] 其中\(\beta_t\)通常取較小正實數。根據該公式定義,前向過程的每一步會將均值向原點收縮,隨後在收縮後的位置疊加隨機噪聲。
式 1有這樣一個性質:不僅每一步加噪過程是正態分佈,而且這些步驟叠加之後,\(t\)時間的樣本\(x_t\)也服從正態分佈。
給定任意的時間步\(t\),我們可以知道\(t\)時間的樣本服從: \[ q(\vx_t | \vx_0) = \N(\vx_t; \sqrt{\bar\alpha_t}\vx_0, (1- \bar\alpha_t)\mI), \tag{2}\] 其中\(\alpha_t := 1 - \beta_t\), \(\bar\alpha_t := \prod^t_{t=1}\alpha_s\).
將式 1重寫得到 \[ q(\vx_t|\vx_{t-1}):=\N (\vx_{t}; \sqrt{\alpha_t}\vx_{t-1}, (1 - \alpha_t) \mI) \]
已知\(\vx_{t-1}\),想要采樣\(\vx_t\),該怎麽做呢?重參數化技巧引入一個隨機變量\(\vec\epsilon^*_{t-1} \sim \N(\mZero,\mI)\),這樣采樣: \[ \vx_t = \sqrt{\alpha_t} \vx_{t-1} + \sqrt{1 - \alpha_t} \vec\epsilon^*_{t-1} \] 這樣做的好處是,如果我們需要,我們可以根據這個式子對\(\vx_{t-1},\alpha_t\)等參數求導。
利用這個技巧,式 2的證明就變得顯然了(以下所有\(\vec\epsilon\)都獨立同分佈地採樣於\(\N(\mZero,\mI)\)): \[ \begin{aligned} \vx_t &= \sqrt{\alpha_t} \vx_{t-1} + \sqrt{1 - \alpha_t} \vec\epsilon^*_{t-1} \\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}\vx_{t-2} + \sqrt{1 - \alpha_{t-1}}\vec\epsilon^*_{t-2}) + \sqrt{1 - \alpha_t} \vec\epsilon^*_{t-1}\\ &= \sqrt{\alpha_t\alpha_{t-1}} \vx_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}} \vec\epsilon^*_{t-2} + \sqrt{1 - \alpha_t}\vec\epsilon^*_{t-1} \\ &\text{兩個高斯變量相加} \\ &= \sqrt{\alpha_t\alpha_{t-1}} \vx_{t-2} + \sqrt{\sqrt{\alpha_t - \alpha_t \alpha_{t-1}}^2 + \sqrt{1 - \alpha_t}^2} \vec\epsilon_{t-2} \\ &= \sqrt{\alpha_t\alpha_{t-1}} \vx_{t-2} + \sqrt{\alpha_t - \alpha_t\alpha_{t-1} + 1 - \alpha_t}\vec\epsilon_{t-2} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \vx_{t-2} + \sqrt{1 - \alpha_t\alpha_{t-1}} \vec\epsilon_{t-2} \\ &= \dots \\ &= \sqrt{\prod_{i=0}^{k}\alpha_{t-i}} \vx_{t-k-1} + \sqrt{1 - \prod_{i=0}^{k}\alpha_{t-i}} \vec\epsilon_{t-k-1} & (\forall k\in[0, t])\\ &= \dots \\ &= \sqrt{\prod_{i=1}^t \alpha_i} \vx_0 + \sqrt{1 - \prod_{i=1}^t\alpha_i}\vec\epsilon_0 \\ &= \sqrt{\bar{\alpha}_t} \vx_0 + \sqrt{1 - \bar{\alpha}_t} \vec\epsilon_0 \\ &\sim \mathcal N(\vx_t; \sqrt{\bar\alpha_t} \vx_0, (1 - \bar\alpha_t)\mI) \end{aligned} \tag{3}\]
因此,利用重參數化技巧,根據式 2有 \[ \vx_t = \sqrt{\bar\alpha_t}\vx_0 + \sqrt{1 - \bar\alpha_t}\vec\epsilon, ~~\text{其中}\vec\epsilon \sim \N(\mZero,\mI) \tag{4}\]
讓我們從一個簡單的情況開始分析。假設我們的樣本空間是一維實數。設\(\vx_0\)的先驗分佈是:有一定的概率是\(-3\),有一定的概率是\(3\). 代碼實現是:
def sample_from_prior():
if np.random.rand() < 0.2: return -3
return 3雖然它很簡單,但是方便我們畫圖,展示擴散的過程。 同時它也是非常貼切的:在無數像素的組合中,只有少數的特定組合排列在人類看來是有意義的;對應到我們的這個例子,在\((-\infty,\infty)\)這個無窮長的數軸上,合理的樣本點只有\(-3\)和\(3\). 圖像生成任務的挑戰性就在於,我們要在無窮的組合中盡可能貼近那些少數的組合,偏離一點都會讓人覺得不真實。
beta = torch.linspace(1e-4, 0.02, T + 1)
alpha = 1 - beta
alpha_bar = torch.cumprod(alpha, dim=0)
def single_step_forward(x_prev, t, epsilon):
'''如果你已知 x_{t-1} ,要採樣 x_t,可以使用這個函數'''
mean = np.sqrt(1 - beta[t]) * x_prev
variance = beta[t]
return mean + epsilon * np.sqrt(variance)
def forward(x0, t, epsilon):
'''如果你已知 x_0 ,要採樣 x_t,不關心中間過程,可以使用這個函數'''
xt = torch.sqrt(alpha_bar[t]) * x0 + torch.sqrt(1 - alpha_bar[t]) * epsilon
return xt 現在我們畫圖看看,看樣本在擴散模型的前向過程中是如何擴散的。
繪圖代碼
import matplotlib.pyplot as plt
def plot_forward():
for trail in range(10):
x_0 = sample_from_prior()
x = [x_0]
for t in range(1, T):
epsilon = np.random.normal()
x.append(single_step_forward(x[-1], t, epsilon))
plt.plot(x, alpha=0.6)
plt.xlabel('t')
plt.ylabel('x')
plt.title('Forward Process')
plt.show()
plot_forward()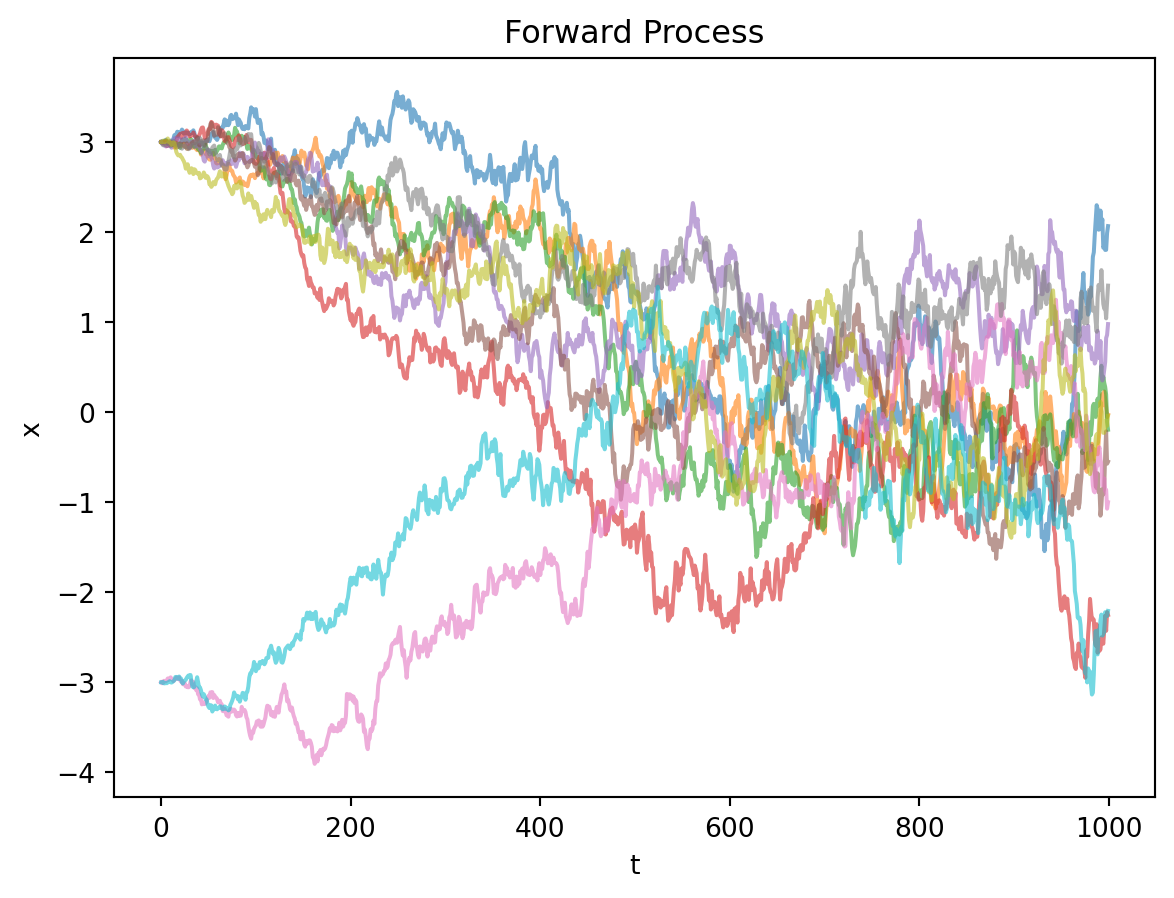
圖的最左端是初始樣本,初始樣本有1/2的概率在+3的位置初始化,也有1/2的概率在-3的位置初始化。但是它們隨著時間\(t\)的推進,最終成為服從標準正態分佈的噪聲。
反向過程
反向過程求的是\(q(\vx_{t-1}|\vx_t)\),但這個式子是難解的,需要我們用一個神經網絡去擬合。設這個近似模型為\(p_\vtheta(\vx_{t-1}|\vx_t)\).
在擴散模型的相關論文中,習慣用\(q\)表示真實的數據分佈,用\(p\)表示模型近似的分佈。
我們將\(p_\vtheta(\vx_{t-1}|\vx_t)\)的近似對象設為\(q(\vx_{t-1}|\vx_{t}, \vx_0)\). (不妨稱\(q(\vx_{t-1}|\vx_{t}, \vx_0)\)為反向過程的真實分佈。)可以證明 \[ q(\vx_{t-1} |\vx_t, \vx_0) = \N(\vx_{t-1}; \tilde \vmu_{t}(\vx_t, \vx_0), \tilde{\beta}_t \mI), \tag{5}\] 其中 \[\tilde \vmu_t(\vx_t, \vx_0):= \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t} \vx_0+\frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\vx_t, \tag{6}\] \[\tilde{\beta_t}:=\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar\alpha_t}\beta_t \tag{7}\]
證明
\[ \begin{aligned} q(\vx_{t-1}|\vx_t, \vx_0) &= \frac{q(\vx_t|\vx_{t-1}, \vx_0) q(\vx_{t-1}|\vx_0)}{q(\vx_t|\vx_0)} \\ &= \frac{\mathcal N(\vx_t; \sqrt{\alpha_t}\vx_{t-1}, (1 - \alpha_t)\mI)\mathcal N(\vx_{t-1}; \sqrt{\bar{\alpha}_{t-1}}\vx_0, (1 - \bar\alpha_{t-1})\mI)}{\mathcal N(\vx_t;\sqrt{\bar\alpha_t}\vx_0, (1 - \bar\alpha_t)\mI)} \\ &\propto \exp\left\{-\left[ \frac{(\vx_t - \sqrt{\alpha_t}\vx_{t-1})^2}{2(1 - \alpha_t)} + \frac{(\vx_{t-1} - \sqrt{\bar\alpha_{t-1}}\vx_0)^2}{2(1 - \bar\alpha_{t-1})} - \frac{(\vx_t - \sqrt{\bar\alpha_t}\vx_0)^2}{2(1 - \bar\alpha_t)} \right] \right\} \\ &= \exp\left\{-\frac{1}{2}\left[ \frac{(\vx_t - \sqrt{\alpha_t}\vx_{t-1})^2}{1 - \alpha_t} + \frac{(\vx_{t-1} - \sqrt{\bar\alpha_{t-1}}\vx_0)^2}{1 - \bar\alpha_{t-1}} - \frac{(\vx_t - \sqrt{\bar\alpha_t}\vx_0)^2}{1 - \bar\alpha_t} \right] \right\} \\ & \text{把與}\vx_t,\vx_0\text{有關的常數項摘出來} \\ &= \exp\left\{ -\frac{1}{2}\left[\frac{-2\sqrt{\alpha_t} \vx_t \vx_{t-1} + \alpha_t \vx^2_{t-1}}{1 - \alpha_t} + \frac{\vx^2_{t-1} - 2\sqrt{\bar\alpha_{t-1}}\vx_{t-1}\vx_0}{1 - \bar\alpha_{t-1}} + C(\vx_t, \vx_0)\right] \right\} \\ &\propto \exp\left\{-\frac{1}{2} \left[ -\frac{2\sqrt{\alpha_t}\vx_t\vx_{t-1}}{1 - \alpha_t} + \frac{\alpha_t\vx^2_{t-1}}{1 - \alpha_t} + \frac{\vx_{t-1}^2}{1 - \bar\alpha_{t-1}} - \frac{2\sqrt{\bar\alpha_{t-1}}\vx_{t-1}\vx_0}{1 - \bar\alpha_{t-1}} \right]\right\} \\ &= \exp\left\{-\frac{1}{2} \left[(\frac{\alpha_t}{1 - \alpha_t} + \frac{1}{1 - \bar\alpha_{t-1}})\vx^2_{t-1} - 2 \left(\frac{\sqrt{\alpha_t}\vx_t}{1 - \alpha_t} + \frac{\sqrt{\bar\alpha_{t-1}}\vx_0}{1 - \bar\alpha_{t-1}}\right)\vx_{t-1}\right] \right\}\\ &= \exp\left\{-\frac{1}{2} \left[\frac{\alpha_t(1 - \bar\alpha_{t-1}) + 1 - \alpha_t}{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}\vx^2_{t-1} - 2 \left(\frac{\sqrt{\alpha_t}\vx_t}{1 - \alpha_t} + \frac{\sqrt{\bar\alpha_{t-1}}\vx_0}{1 - \bar\alpha_{t-1}}\right)\vx_{t-1}\right] \right\}\\ &\text{注意}\alpha_t \bar\alpha_{t-1} = \bar\alpha_t \\ &= \exp\left\{-\frac{1}{2} \left[\frac{1 - \bar\alpha_t}{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}\vx^2_{t-1} - 2 \left(\frac{\sqrt{\alpha_t}\vx_t}{1 - \alpha_t} + \frac{\sqrt{\bar\alpha_{t-1}}\vx_0}{1 - \bar\alpha_{t-1}}\right)\vx_{t-1}\right] \right\}\\ &= \exp\left\{ -\frac{1}{2} \left(\frac{1 - \bar\alpha_t}{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}\right)\left[\vx_{t-1}^2 - 2 \frac{ \left(\frac{\sqrt{\alpha_t}\vx_t}{1 - \alpha_t} + \frac{\sqrt{\bar\alpha_{t-1}}\vx_0}{1 - \bar\alpha_{t-1}}\right)}{\frac{1 - \bar\alpha_t}{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}}\vx_{t-1}\right] \right\}\\ &= \exp\left\{ -\frac{1}{2} \left(\frac{1 - \bar\alpha_t}{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}\right)\left[\vx_{t-1}^2 - 2 \frac{ \left(\frac{\sqrt{\alpha_t}\vx_t}{1 - \alpha_t} + \frac{\sqrt{\bar\alpha_{t-1}}\vx_0}{1 - \bar\alpha_{t-1}}\right)(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\vx_{t-1}\right] \right\}\\ &= \exp\left\{ -\frac{1}{2} \left(\frac{1}{\frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}}\right)\left[\vx_{t-1}^2 - 2 \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})\vx_t + \sqrt{\bar\alpha_{t-1}}(1 - \alpha_t)\vx_0}{1 - \bar\alpha_t}\vx_{t-1}\right] \right\}\\ &\propto \mathcal N(\vx_{t-1}; \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})\vx_t + \sqrt{\bar\alpha_{t-1}}(1 - \alpha_t)\vx_0}{1 - \bar\alpha_t},\frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\mI) \\ &= \mathcal N(\vx_{t-1}; \frac{\sqrt{\bar\alpha_{t-1}}\beta_t\vx_0 + \sqrt{\alpha_t}(1 - \bar\alpha_{t-1})\vx_t}{1 - \bar\alpha_t},\frac{(\beta_t)(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\mI) \end{aligned} \tag{8}\]接著考慮模型\(p_\vtheta(\vx_{t-1}|\vx)\)的設計,設其為一個正態分佈\(\N(\vx_{t-1};\vmu_\vtheta(\vx_t, t), \mSigma_\vtheta(\vx_t, t))\).
\(\mSigma_\vtheta(\vx_t, t)=\sigma_t^2\mI\)有兩種選擇,一種是設\(\sigma_t^2=\beta_t\);另一種是設\(\sigma_t^2=\tilde \beta_t\)。論文[1]表示兩種選擇的效果差不多。為什麼協方差矩陣有兩種選擇
這個坑留著以後再填😼至於\(\vmu_\vtheta(\vx_t, t)\)的設計,通過將\(\vx_0\)的預測值填入式 6即可得到。但是DDPM採取了一種間接的方法,預測噪聲\(\vepsilon\),然後代入式 3得到\(\vx_0\),從而可以推導出: \[\vmu_\vtheta(\vx_t, t)=\frac{1}{\sqrt{\alpha_t}}\left(\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\vec\epsilon_\vtheta(\vx_t, t)\right), \tag{9}\] 論文[1]表示這樣做效果比較好。
式 9的證明
由式 3可得 \[ \vx_0 = \frac{1}{\sqrt{\bar\alpha_t}}(\vx_t - \sqrt{1 - \bar\alpha_t}\vepsilon) \] 代入\(\tilde\vmu_t\)的定義: \[ \begin{aligned} \tilde\vmu_t (\vx_t, \vx_0) &= \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t} \vx_0 + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\vx_t \\ &= \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t} \left(\frac{1}{\sqrt{\bar\alpha_t}}(\vx_t - \sqrt{1 - \bar\alpha_t}\vepsilon)\right) + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\vx_t \\ &= \frac{\beta_t}{(1 - \bar\alpha_t)\sqrt{\alpha_t}}\left(\vx_t - \sqrt{1 - \bar\alpha_t}\vepsilon \right) + \frac{{\alpha_t}(1 - \bar\alpha_{t-1})}{(1 - \bar\alpha_t)\sqrt{\alpha_t}}\vx_t \\ &= \frac{\beta_t + \alpha_t(1 - \bar\alpha_{t-1})}{(1 - \bar\alpha_t)\sqrt{\alpha_t}} \vx_t - \frac{\beta_t\sqrt{1 - \bar\alpha_t}}{(1 - \bar\alpha_t)\sqrt{\alpha_t}}\vepsilon\\ &= \frac{1}{\sqrt{\alpha_t}}\left(\frac{\beta_t + \alpha_t - \bar\alpha_t}{1 - \bar\alpha_t}\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\vepsilon\right)\\ &= \frac{1}{\sqrt{\alpha_t}}\left(\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\vepsilon\right) \end{aligned}, \] 將上式中的\(\vepsilon\)替換為模型預測的噪聲,就得到了式 9我設計了下面這樣的一個Pytorch模型來實現式 9。模型結構和細節是隨便拍的。
import torch
import torch.nn as nn
class Theta(nn.Module):
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(8, 8),
nn.ReLU(),
nn.Linear(8, 1),
nn.Tanh()
)
def forward(self, xt, t):
return pred_noise(self, xt, t)
def pred_noise(theta, xt, t):
t = t / T
# 為了便於模型學習,增加了一些特徵比如x_t * t
vx = torch.stack([t, t**2, t**3, xt, xt**2, xt**3, xt*t, xt*t**2]).float().permute(1, 0)
ret = theta.layers(vx) * 3
bs, dim = ret.shape
assert dim == 1
return ret.flatten()優化目標
優化目標是最大化似然,即最小化: \[ \begin{aligned} \E[-\log p_\vtheta(\vx_0)] &\leq \E_q\left[-\log \frac{p_\vtheta(\vx_{0:T})}{q(\vx_{1:T}|\vx_0)}\right] \\ &=\E_q\left[-\log p(\vx_T) - \sum_{t\geq 1} \log \frac{p_\vtheta(\vx_{t-1}|\vx_t)}{q(\vx_t|\vx_{t-1})}\right] \\ &=: L \\ \end{aligned} \] \(L\)
可以簡化為: \[ L_\text{simple}(\vtheta) := \E_{t, \vx_0, \vec\epsilon}\left [ \Vert \vec\epsilon - \vec\epsilon_\vtheta(\vx_t, t) \Vert^2 \right] \tag{10}\]
\[ \begin{aligned} L &= \E_q\left[-\log \frac{p_\vtheta(\vx_{0:T})}{q(\vx_{1:T}|\vx_0)}\right] \\ &=\E_q\left[-\log p(\vx_T) - \sum_{t\geq 1} \log \frac{p_\vtheta(\vx_{t-1}|\vx_t)}{q(\vx_t|\vx_{t-1})}\right] \\ &= \E_q\left[-\log p(\vx_T) - \sum_{t>1}\log \frac{p_\vtheta(\vx_{t-1}|\vx_t)}{q(\vx_t|\vx_{t-1})}-\log \frac{p_\vtheta(\vx_0|\vx_1)}{q(\vx_1|\vx_0)}\right] \\ & \left(\text{注意到}q(\vx_t|\vx_{t-1}) = {q(\vx_{t-1}|\vx_t, \vx_0)\cdot q(\vx_{t}|\vx_0)\over q(\vx_{t-1}|\vx_0)}\right)\\ &= \E_q\left[ -\log p(\vx_T) - \sum_{t>1} \log \left(\frac{p_\vtheta(\vx_{t-1}|\vx_t)}{q(\vx_{t-1}|\vx_t, \vx_0)}\cdot \frac{\color{red}q(\vx_{t-1}|\vx_0)}{\color{red} q(\vx_t|\vx_0)}\right) - \log \frac{p_\vtheta(\vx_0|\vx_1)}{q(\vx_1|\vx_0)} \right] \\ & \left(求和式的紅色部分,中間項會與相鄰項相互抵消\right)\\ &= \E_q\left[ -\log \frac{p(\vx_T)}{q(\vx_T|\vx_0)} - \sum_{t>1}\log \frac{p_\vtheta(\vx_{t-1}|\vx_t)}{q(\vx_{t-1}|\vx_t, \vx_0)} - \log p_\vtheta(\vx_0|\vx_1 ) \right]\\ &= \E_q\left[ \underbrace{{\KL(q(\vx_T|\vx_0)\Vert p(\vx_T))}}_{L_T} + \sum_{t>1} \underbrace{\KL(q(\vx_{t-1}|\vx_t, \vx_0)\Vert p_\vtheta(\vx_{t-1}|\vx_t))}_{L_{t-1}} - \underbrace{\log p_\vtheta(\vx_0|\vx_1)}_{L_0} \right]\\ \end{aligned} \tag{11}\]
可以看到損失分為三部分:
- \(L_T\):由於\(p(\vx_T)\)被設計為標準正態分佈,沒有任何可學習參數,因此\(L_T\)為常量,不影響模型訓練。
- \(L_0\):\(L_0\)本可以合併到\(L_{t-1}\)中去,但為什麼要把它單獨拎出來討論呢?因為\(\vx_0\)作為圖像經常是離散的,其像素值可能是0~255的整數。可能需要我們特殊對待。當然你也可以不在乎這種細節,那麼\(L_0\)就和\(L_{t-1}\)沒什麼區別。
- 接下來我們討論\(L_{t-1}\)。
根據多元高斯分佈的KL散度公式,有: \[ L_{t-1} \doteq \E_q\left[ \frac{1}{2\sigma_t^2} \Vert \tilde \vmu_t(\vx_t, \vx_0) - \vmu_\vtheta(\vx_t, t) \Vert^2 \right] \] 其中\(\doteq\)表示左右相差一個常數。
前面提到模型被設計為預測噪聲\(\vepsilon\),套用式 9,得到 \[ \begin{aligned} L_{t-1} &\doteq \E_{\vx_0,\vepsilon} \left[\frac{1}{2\sigma_t^2} \left\Vert \frac{1}{\sqrt{\alpha_t}} (\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}} \vepsilon_\vtheta(\vx_t, t)) - \frac{1}{\sqrt{\alpha_t}} (\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}} \vepsilon) \right\Vert^2\right]\\ &= \E_{\vx_0, \vepsilon} \left[\frac{1}{2\sigma_t^2} \left\Vert \frac{\beta_t}{\sqrt{\alpha_t}\sqrt{1 - \bar\alpha_t}} (\vepsilon - \vepsilon_\vtheta(\vx_t, t)) \right\Vert^2\right]\\ &= \E_{\vx_0, \vepsilon} \left[\frac{\beta_t^2}{2\sigma_t^2\alpha_t (1 - \bar\alpha_t)} \left\Vert (\vepsilon - \vepsilon_\vtheta(\vx_t, t)) \right\Vert^2\right]\\ \end{aligned} \tag{12}\]
這是一個帶權重版本的式 10,權重取決於\(t\). 但是論文[1]表明去掉權重的式 10更能鼓勵模型學習高噪聲條件下的預測任務。
至此,我們就解釋了式 10是怎麼來的。
現在我們已經有了損失函數,那麽就開始訓練吧。
因爲模型很小,問題簡單,因此訓練很快,只需要幾十秒就能完成。
模型訓練
loss_list = []
lr = 5e-3
batch_size = 8092
theta = Theta()
for it in range(10000):
x0 = torch.tensor([sample_from_prior() for _ in range(batch_size)])
t = torch.randint(1, T, size=(batch_size,))
epsilon = torch.randn(batch_size)
xt = forward(x0, t, epsilon)
pred_epsilon = pred_noise(theta, xt, t)
loss = torch.mean((epsilon - pred_epsilon)**2)
loss.backward()
with torch.no_grad():
for p in theta.parameters():
if not p.requires_grad: continue
p -= lr * p.grad
p.grad.zero_()
loss_list.append(loss.item())訓練損失曲綫
plt.plot(loss_list)
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.show()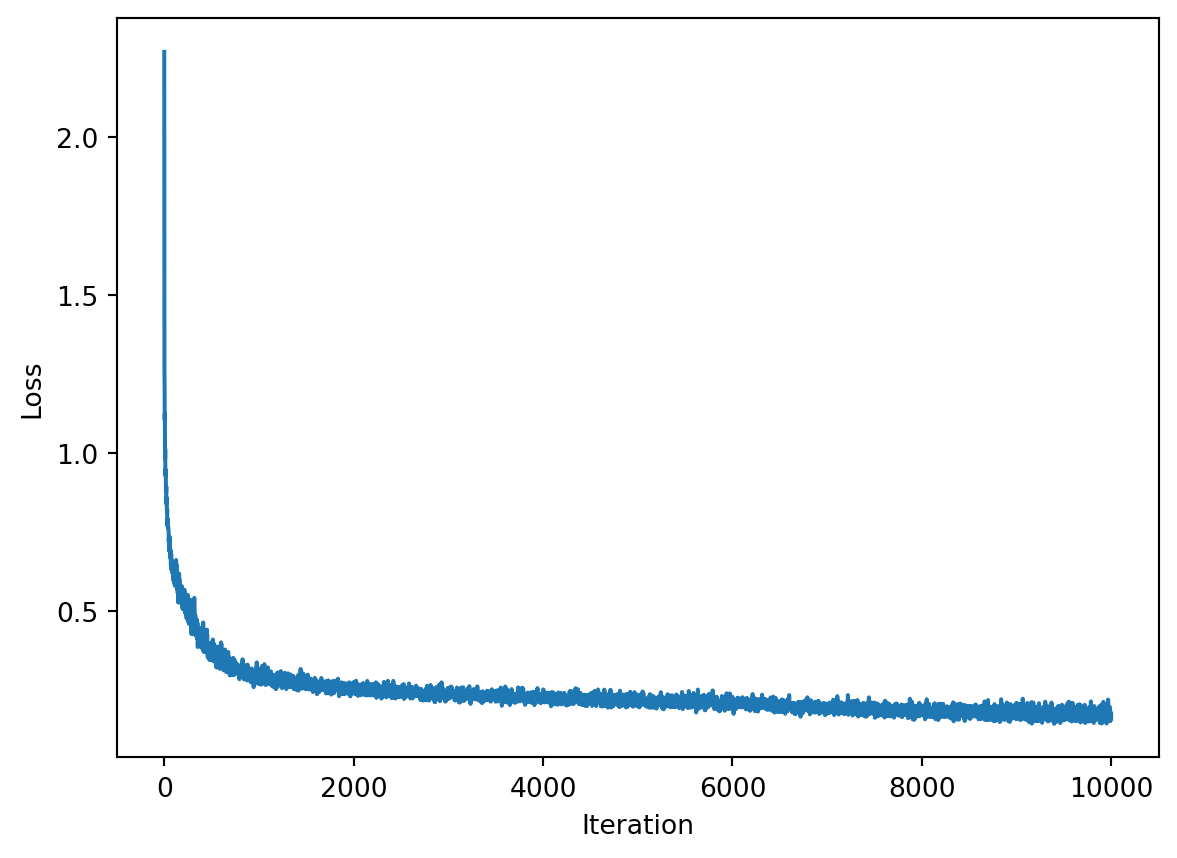
採樣
現在我們已經訓練好了模型,接下來就可以採樣了。採樣的過程是從\(t=T\)開始,利用式 9,逐步向\(t=0\)反向推進。
輸入\(\vx_t\)和對噪聲的預測,計算\(\vx_{t-1}\)的方式實現如下:
from typing import Literal
def ddpm_backward(
xt,
noise_pred,
tau,
i,
):
assert i > 0
t = tau[i]
t_prev = tau[i - 1]
sigma_t_sq = (1 - alpha_bar[t - 1]) / (1 - alpha_bar[t]) * beta[t]
# sigma_t_sq = beta[t]
xt_prev = 1 / torch.sqrt(alpha[t]) * (xt - (1 - alpha[t]) / torch.sqrt(1 - alpha_bar[t]) * noise_pred) + sigma_t_sq**0.5 * torch.randn_like(xt)
return xt_prev 接著我們代入我們訓練好的模型來預測噪聲,採樣鏈路就通了。
@torch.inference_mode()
def denoise(t, batch_size, xT):
if t == T: return [(T, xT)]
tau = list(range(T + 1))
t_next = tau[tau.index(t) + 1]
(_, x_next), *history = denoise(t_next, batch_size, xT)
epsilon = pred_noise(theta, x_next, torch.ones(batch_size) * t_next)
x_t = ddpm_backward(x_next, epsilon, tau, tau.index(t) + 1)
return [(t, x_t), (t_next, x_next), *history]
batch_size = 50
xT = torch.randn(batch_size)
sample_trace = denoise(0, batch_size, xT=xT)繪圖代碼
for b in range(batch_size):
plt.plot([it[0] for it in sample_trace], [it[1][b] for it in sample_trace], alpha=0.2)
# x軸反轉
plt.xlim(T, 0)
plt.xlabel('t')
plt.ylabel('x')
plt.show()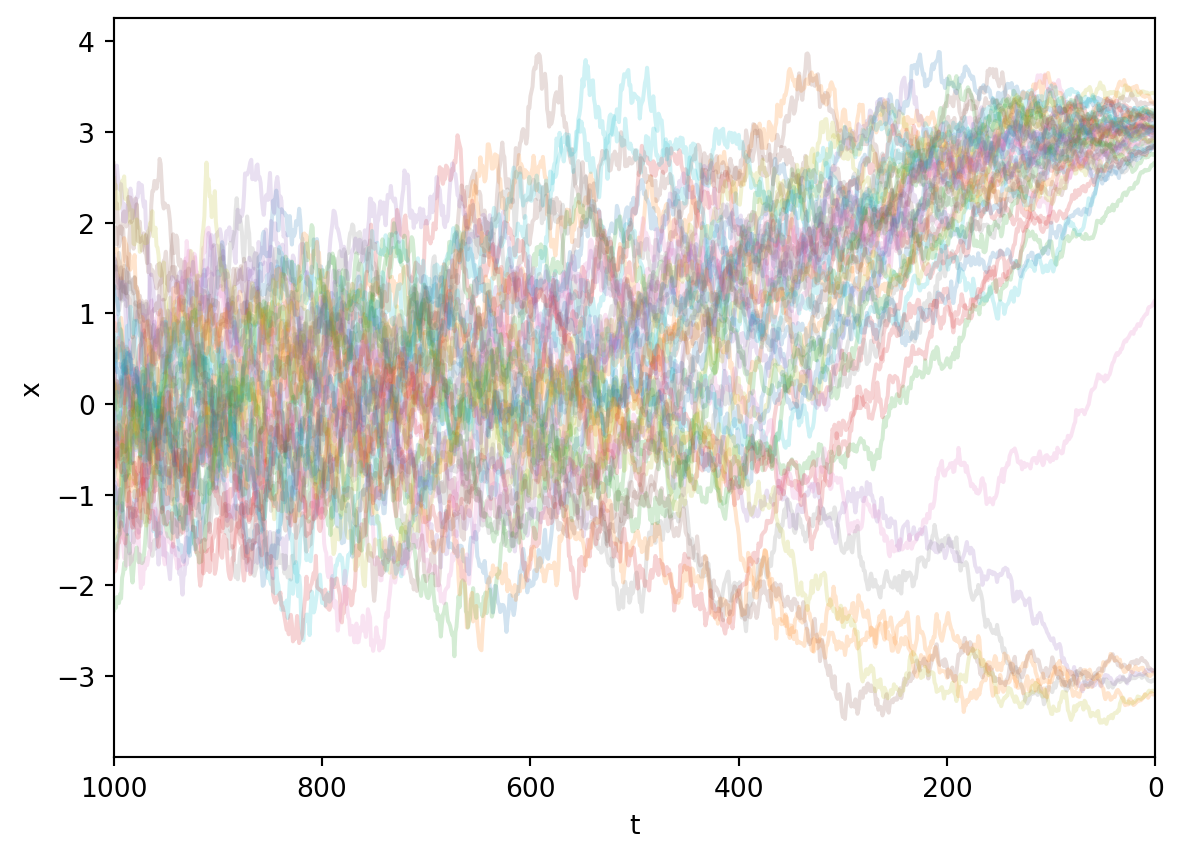
用我們訓練好的模型,可以繪製出如圖所示的採樣過程。可以看到,出發點服從標準正態分佈。對於任意出發點,模型都很好地給出了一條反向去噪路線,最終把它們推到一個合適的終點。
DDPM的採樣可以跳步嗎
在訓練的時候,我們設置了\(T=1000\)的擴散步長,這使得我們在採樣的時候也得採樣\(1000\)步。對於真實的任務,這會非常花時間。
但是,很幸運,DDPM的採樣是可以跳步的。
回想起我們是怎麼訓練和採樣的。我們以\(\vx_t\)和\(t\)作為輸入,預測\(\vx_0\)。然後我們以預測的\(\vx_0\)代入式 6得到對\(\vx_{t-1}\)的預測. 這一套流程完全可以推廣到跳步採樣的情形。
我們仔細觀察式 9(複製粘貼到這): \[ \vmu_\vtheta(\vx_t, t)=\frac{1}{\sqrt{\alpha_t}}\left(\vx_t - \frac{\beta_t}{\sqrt{1 - \bar\alpha_t}}\vec\epsilon_\vtheta(\vx_t, t)\right) \]
注意到公式使用了\(\alpha_t\)和\(\beta_t = 1 - \alpha_t\),而\(\alpha_t = {\bar\alpha_t\over \bar\alpha_{t-1}}\).
顯然,只要我們將所有的\(\alpha_t\)替換為\({\bar\alpha_t \over \bar\alpha_{t-k}}\),就可以得到跳\(k\)步採樣時的公式。
據此,我可以寫出如下的跳步採樣邏輯(使用先前訓練好的模型,但是只在採樣的時候跳步)。
def ddpm_backward(
xt,
noise_pred,
tau,
i,
):
'''
DDPM的跳步採樣策略。
這裡tau是一個[0, 1, 2, 3, ... T]的子序列,例如
[0, 2, 4, 6, ..., T],決定了如何跳步
'''
assert i > 0
t = tau[i]
t_prev = tau[i - 1]
alpha_prod = alpha_bar[t] / alpha_bar[t_prev]
sigma_t_sq = (1 - alpha_bar[t_prev]) / (1 - alpha_bar[t]) * (1 - alpha_prod)
xt_prev = 1 / torch.sqrt(alpha_prod) * (xt - (1 - alpha_prod) / torch.sqrt(1 - alpha_bar[t]) * noise_pred) + sigma_t_sq**0.5 * torch.randn_like(xt)
return xt_prev
@torch.inference_mode()
def denoise(t, batch_size, step_size, xT):
# 該函數示範了如何利用ddpm_backward進行採樣。
if t == T: return [(T, xT)]
tau = list(range(T))[::step_size] + [T]
t_next = tau[tau.index(t) + 1]
(_, x_next), *history = denoise(t_next, batch_size, step_size, xT)
epsilon = pred_noise(theta, x_next, torch.ones(batch_size) * t_next)
x_t = ddpm_backward(x_next, epsilon, tau, tau.index(t) + 1)
return [(t, x_t), (t_next, x_next), *history]下面的圖像顯示了,訓練好的DDPM模型允許我們在採樣時跳步,但不損失太多採樣質量。
繪圖代碼
def plot_denoise(step_size):
sample_trace = denoise(0, batch_size, step_size=step_size, xT=xT)
ax = plt.gca()
for b in range(batch_size):
ax.plot(
[it[0] for it in sample_trace],
[it[1][b] for it in sample_trace],
alpha=0.2
)
# x軸反轉
ax.set_ylim(-4, 4)
ax.set_xlim(T, 0)
ax.set_xlabel('t')
ax.set_ylabel('x')
ax.set_title(f'step size = {step_size}')
plt.figure(figsize=(16, 8))
plt.subplot(241)
plot_denoise(1)
plt.subplot(242)
plot_denoise(2)
plt.subplot(243)
plot_denoise(4)
plt.subplot(244)
plot_denoise(8)
plt.subplot(245)
plot_denoise(16)
plt.subplot(246)
plot_denoise(32)
plt.subplot(247)
plot_denoise(64)
plt.subplot(248)
plot_denoise(128)
plt.show()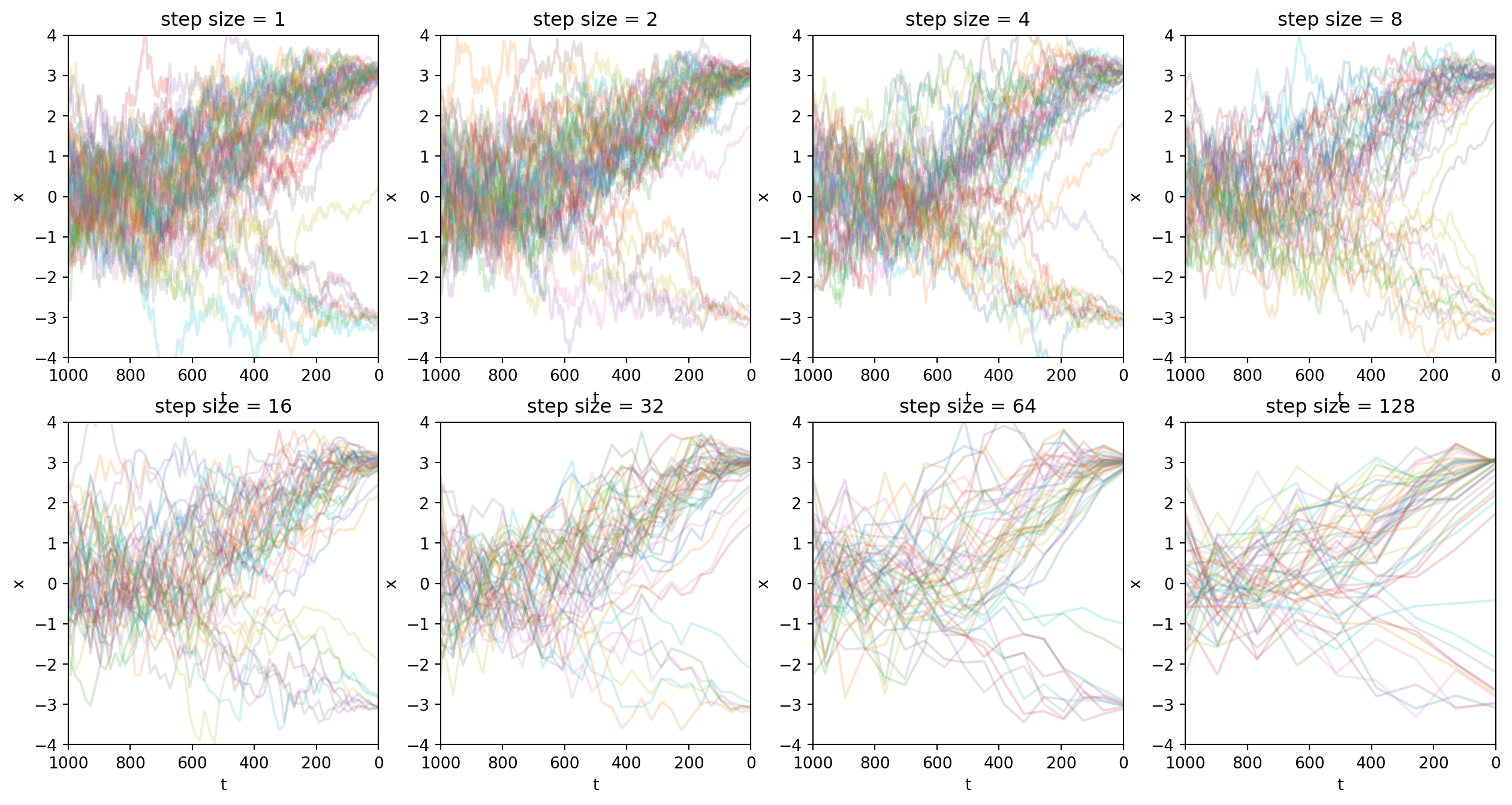
到此,我說明了DDPM的一種可行的跳步技巧。我想借這個簡單的分析引出DDIM這篇文章。我們將會看到對DDPM模型的採樣不必局限於原論文的馬爾科夫鏈的形式。
DDIM
回想起DDPM首先假設\(q(\vx_t|\vx_0, \vx_1, \dots, \vx_{t-1}) = q(\vx_t|\vx_{t-1})\),並且規定了\(q(\vx_t|\vx_{t-1})\)的具體形式,然後得到\(q(\vx_t|\vx_0) = \N(\vx_t; \sqrt{\bar\alpha_t}\vx_0, (1 - \bar\alpha_t)\mI).\) 但是反過來思考,對於同一個\(q(\vx_t|\vx_0)\),前向過程可以有很多種。
例如我們先前討論了從\(\vx_{t-k}\)到\(\vx_t\)的跳步。我們完全可以認為\(\vx_t\)是直接由\(\vx_{t-k}\)生成的,而\(t-k\)和\(t\)之間的樣本並不存在。這並不會改變\(q(\vx_t|\vx_0).\)
前向過程甚至不必是馬爾科夫過程,比如可以是\(q(\vx_t|\vx_{t-1}, \vx_0)\)的形式。
前向過程
綜上所述,DDIM只關心邊際分佈為 \[q(\vx_t|\vx_0) = \N(\vx_t; \sqrt{\bar\alpha_t}\vx_0, (1 - \bar\alpha_t)\mI)\] 的擴散模型。只要邊際分佈滿足這個條件,前向過程的具體形式不重要。
反向過程
和DDPM一樣,DDIM同樣是先給出\(q(\vx_{t-1}|\vx_t, \vx_0)\),然後用\(p_\vtheta(\vx_{t-1}|\vx_t)\)去擬合它。
因為DDIM不假設\(q(\vx_t|\vx_{t-1})\)的具體形式,所以\(q(\vx_{t-1}|\vx_t, \vx_0)\)推導方式和DDPM的區別很大。這裡先引用一些有用的公式。
此處摘錄PRML一書中2.115節的相關結論如下:
如果已知 \[ \begin{aligned} p(\vx) &= \N(\vx|\vmu, \Lambda^{-1})\\ p(\vy|\vx) &= \N(\vy|A\vx+\vec b , L^{-1}) \end{aligned} \] 那麼 \[ p(\vy) = \N(\vy|A\vmu+\vec b, L^{-1} + A\Lambda^{-1}A^T) \]
根據這個結論,我們嘗試回答這個問題:
已知 \[ q(\vx_t| \vx_0) = \N(\vx_t; \sqrt{\bar\alpha_t}\vx_0, (1- \bar\alpha_t)\mI) \] 和 \[ q(\vx_{t-1}|\vx_0) = \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0, (1- \bar\alpha_{t-1})\mI), \] 問\(q(\vx_{t-1}|\vx_t, \vx_0)\)應該是什麼?
假設 \[ q(\vx_{t-1}|\vx_t, \vx_0) := \N(\vx_{t-1}; A\vx_t + \vec b, \Sigma_3), \] 但是\(A,\vec b,\Sigma_3\)是矩陣或者向量,參數太多。為了使方程有解,我們需要減少未知參數量,改為這樣構造 \[ q(\vx_{t-1}|\vx_t, \vx_0) := \N(\vx_{t-1}; a\vx_t + b, \sigma_t^2\mI). ~~(a > 0) \tag{13}\] 於是我們可以得到這樣的方程。 \[ \left\{ \begin{aligned} \sqrt{\bar\alpha_{t-1}} &= a\sqrt{\bar\alpha_t} + b, \\ (1 - \bar\alpha_{t-1}) \mI &= \sigma_t^2\mI + a^2 (1 - \bar\alpha_t) \mI, \end{aligned} \right. \] 假設\(\sigma_t\)是一個由我們自行決定的參數,那麼未知數就只有\(a\)和\(b\). 解得 \[ \left\{ \begin{aligned} a &= \sqrt{\frac{1 - \bar\alpha_{t-1} - \sigma_t^2}{1 - \bar\alpha_t}} \\ b &= \left( \sqrt{\bar\alpha_{t-1}} - \sqrt{\frac{1 - \bar\alpha_{t-1} - \sigma_t^2}{1 - \bar\alpha_t}}\sqrt{\bar\alpha_t} \right)\vx_0 \end{aligned} \right. \]
代入式 13,得 \[ \begin{aligned} q(\vx_{t-1}|\vx_t, \vx_0) &= \N(\vx_{t-1}; a\vx_t + b, \sigma_t^2\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \sqrt{\frac{1 - \bar\alpha_{t-1} - \sigma_t^2}{1 - \bar\alpha_t}}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \sigma_t^2\mI) \\ \end{aligned} \]
就像DDPM做的那樣,將上式中的\(\vx_0\)替換為我們的預測值,我們就可以構造出從\(\vx_t\)到\(\vx_{t-1}\)的反向過程。可以直接預測\(\vx_0\),也可以通過預測\(\vepsilon\)間接預測\(\vx_0\).
我們說DDPM是DDIM的特例。將\(\sigma_t^2\)設為\(\tilde{\beta_t}:=\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar\alpha_t}\beta_t\),我們就能看到這一點。這個時候
\[ \begin{aligned} q(\vx_{t-1}|\vx_t, \vx_0) &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \sqrt{\frac{1 - \bar\alpha_{t-1} - \sigma_t^2}{1 - \bar\alpha_t}}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \sigma_t^2\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \sqrt{\frac{1 - \bar\alpha_{t-1} - \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar\alpha_t}\beta_t}{1 - \bar\alpha_t}}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \frac{\sqrt{{(1 - \bar\alpha_{t-1})(1 - \bar\alpha_t)- (1 - \bar{\alpha}_{t-1})\beta_t}}}{1 - \bar\alpha_t}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \frac{\sqrt{{(1 - \bar\alpha_{t-1})(1 - \bar\alpha_t)- (1 - \bar{\alpha}_{t-1})(1 - \alpha_t)}}}{1 - \bar\alpha_t}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \frac{\sqrt{(1 - \bar\alpha_{t-1})(\alpha_t - \bar\alpha_t)}}{1 - \bar\alpha_t}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + \frac{\sqrt{(1 - \bar\alpha_{t-1})(1 - \bar\alpha_{t-1})\alpha_t}}{1 - \bar\alpha_t}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \sqrt{\bar\alpha_{t-1}}\vx_0 + (1 - \bar\alpha_{t-1}) \frac{\sqrt{\alpha_t}}{1 - \bar\alpha_t}(\vx_t - \sqrt{\bar\alpha_t}\vx_0), \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \left(\sqrt{\bar\alpha_{t-1}} - \frac{(1 - \bar\alpha_{t-1})\sqrt{\alpha_t}\sqrt{\bar\alpha_t}}{1 - \bar\alpha_t}\right)\vx_0 + (1 - \bar\alpha_{t-1}) \frac{\sqrt{\alpha_t}}{1 - \bar\alpha_t}\vx_t , \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \left(\sqrt{\bar\alpha_{t-1}} - \frac{(\alpha_t - \bar\alpha_{t})\sqrt{\bar\alpha_{t-1}}}{1 - \bar\alpha_t}\right)\vx_0 + (1 - \bar\alpha_{t-1}) \frac{\sqrt{\alpha_t}}{1 - \bar\alpha_t}\vx_t , \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \frac{(1 - \alpha_t)\sqrt{\bar\alpha_{t-1}}}{1 - \bar\alpha_t}\vx_0 + (1 - \bar\alpha_{t-1}) \frac{\sqrt{\alpha_t}}{1 - \bar\alpha_t}\vx_t , \tilde{\beta_t}\mI) \\ &= \N(\vx_{t-1}; \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar\alpha_t}\vx_0 + \frac{\sqrt{\alpha_t}(1 - \bar\alpha_{t-1})}{1 - \bar\alpha_t}\vx_t , \tilde{\beta_t}\mI) \\ \end{aligned} \]
總而言之,DDIM在反向過程中引入了一個\(\sigma_t\)作為參數。而DDPM是\(\sigma^2_t = \tilde{\beta}_t\)時的特例。
那麼,\(\sigma_t\)參數的選擇是否影響優化目標?是否需要我們重新訓練DDPM模型呢?
優化目標
簡單來說,重新選擇\(\sigma_t\)參數不需要重新訓練DDPM模型。因為DDPM的訓練目標是以\(\vx_t\)和\(t\)作為輸入,預測\(\vx_0\). 只要\(\vx_t\)的分佈沒有改變,那就不需要重新訓練。
唯一的區別是,\(\sigma_t\)可能會影響不同時刻的損失的權重。類似式 12的討論,\(\sigma_t\)可能會出現在權重項中。但是同樣的,我們在實際的簡化版損失函數中會將權重刪除。
採樣
接下來,我們用代碼實現DDIM的採樣過程。 和前面一樣,我們會特別關注在子序列tau上的跳步採樣。
同時,正如DDIM特地指出的,\(sigma_t\)可以有各種不同的選擇。例如\(\sigma_t\)可以取為0,這時候採樣過程將會完全失去隨機性。
from typing import Literal
def ddim_backward(
xt,
noise_pred,
tau,
i,
sigma_style : Literal["ddpm", "ddim"]
):
assert i > 0
t = tau[i]
t_prev = tau[i - 1]
alpha_prod = alpha_bar[t] / alpha_bar[t_prev]
tilde_beta = (1 - alpha_bar[t_prev]) / (1 - alpha_bar[t]) * (1 - alpha_prod)
# 我們允許sigma_t取0
sigma_t_sq = tilde_beta if sigma_style == 'ddpm' else 0
x0_pred = (xt - (1 - alpha_bar[t])**0.5 * noise_pred) / (alpha_bar[t]**0.5)
xt_prev = (
# 1. 對x0的預測
alpha_bar[t_prev]**0.5 * x0_pred
# 2. 從x0到xt的向量
+ max(0, 1 - alpha_bar[t_prev] - sigma_t_sq)**0.5 * noise_pred
# 3. 隨機噪聲
+ sigma_t_sq**0.5 * torch.randn_like(xt)
)
return xt_prev 同樣地,我們基於ddim_backward實現一個完整的denoise過程:
@torch.inference_mode()
def denoise(t, batch_size, step_size, xT, sigma_style='ddpm'):
if t == T: return [(T, xT)]
tau = list(range(T))[::step_size] + [T]
t_next = tau[tau.index(t) + 1]
(_, x_next), *history = denoise(t_next, batch_size, step_size, xT, sigma_style)
epsilon = pred_noise(theta, x_next, torch.ones(batch_size) * t_next)
x_t = ddim_backward(x_next, epsilon, tau, tau.index(t) + 1, sigma_style=sigma_style)
return [(t, x_t), (t_next, x_next), *history]
# 用法如下
batch_size = 50
xT = torch.randn(batch_size)
sample_trace_1 = denoise(0, batch_size, step_size=1, xT=xT)至此我們就實現了DDIM採樣。這裡繪製一張圖來展示採樣過程。
繪圖代碼
def plot_denoise(step_size, sigma_style='ddpm'):
sample_trace = denoise(0, batch_size, step_size=step_size, xT=xT, sigma_style=sigma_style)
ax = plt.gca()
for b in range(batch_size):
ax.plot(
[it[0] for it in sample_trace],
[it[1][b] for it in sample_trace],
alpha=0.2
)
# x軸反轉
ax.set_ylim(-4, 4)
ax.set_xlim(T, 0)
ax.set_xlabel('t')
ax.set_ylabel('x')
ax.set_title(f'step size = {step_size}')
plt.figure()
plot_denoise(1)
plt.show()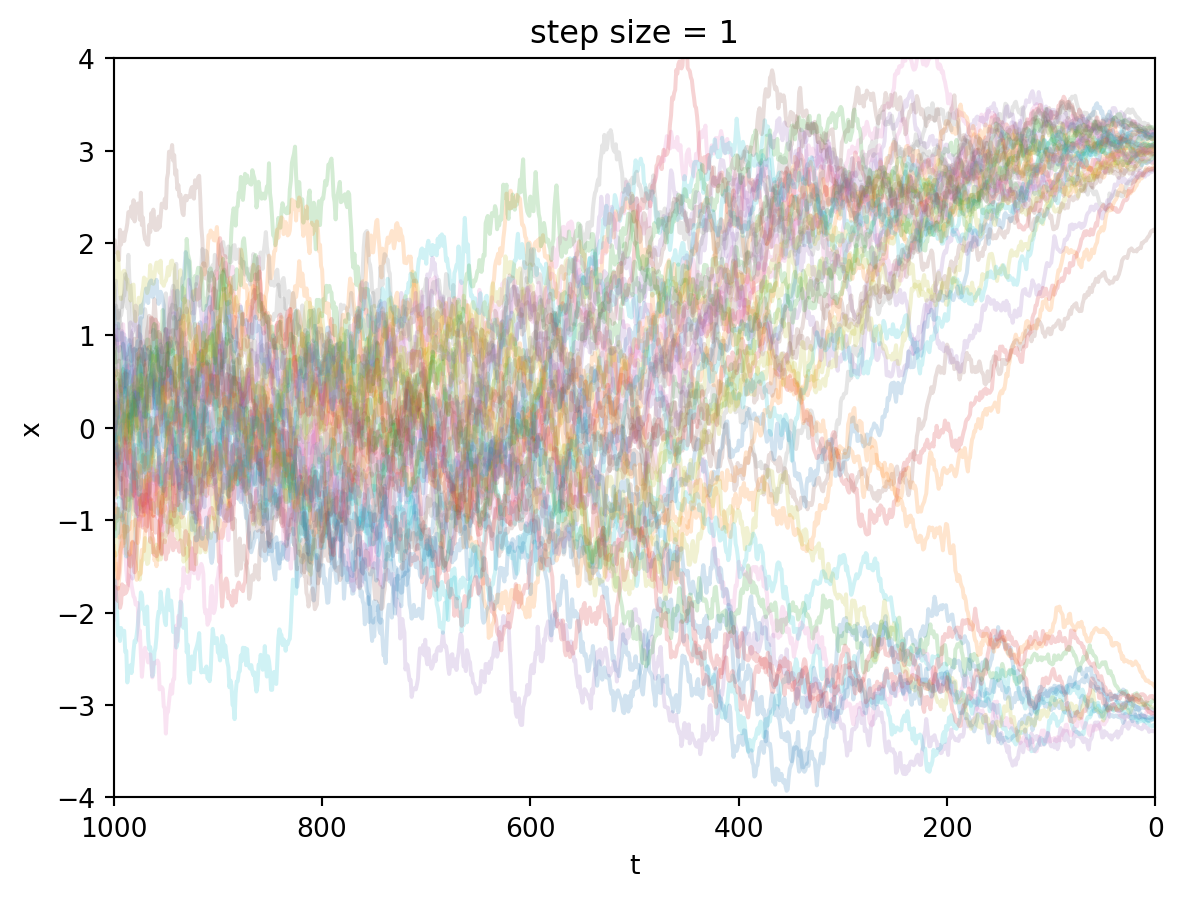
這裡再重複展示一次跳步採樣。跳步採樣是DDIM論文的貢獻之一。(但是在我看來比較顯然)
繪圖代碼
plt.figure(figsize=(16, 8))
plt.subplot(241)
plot_denoise(2)
plt.subplot(242)
plot_denoise(4)
plt.subplot(243)
plot_denoise(8)
plt.subplot(244)
plot_denoise(16)
plt.subplot(245)
plot_denoise(32)
plt.subplot(246)
plot_denoise(64)
plt.subplot(247)
plot_denoise(128)
plt.subplot(248)
plot_denoise(256)
plt.show()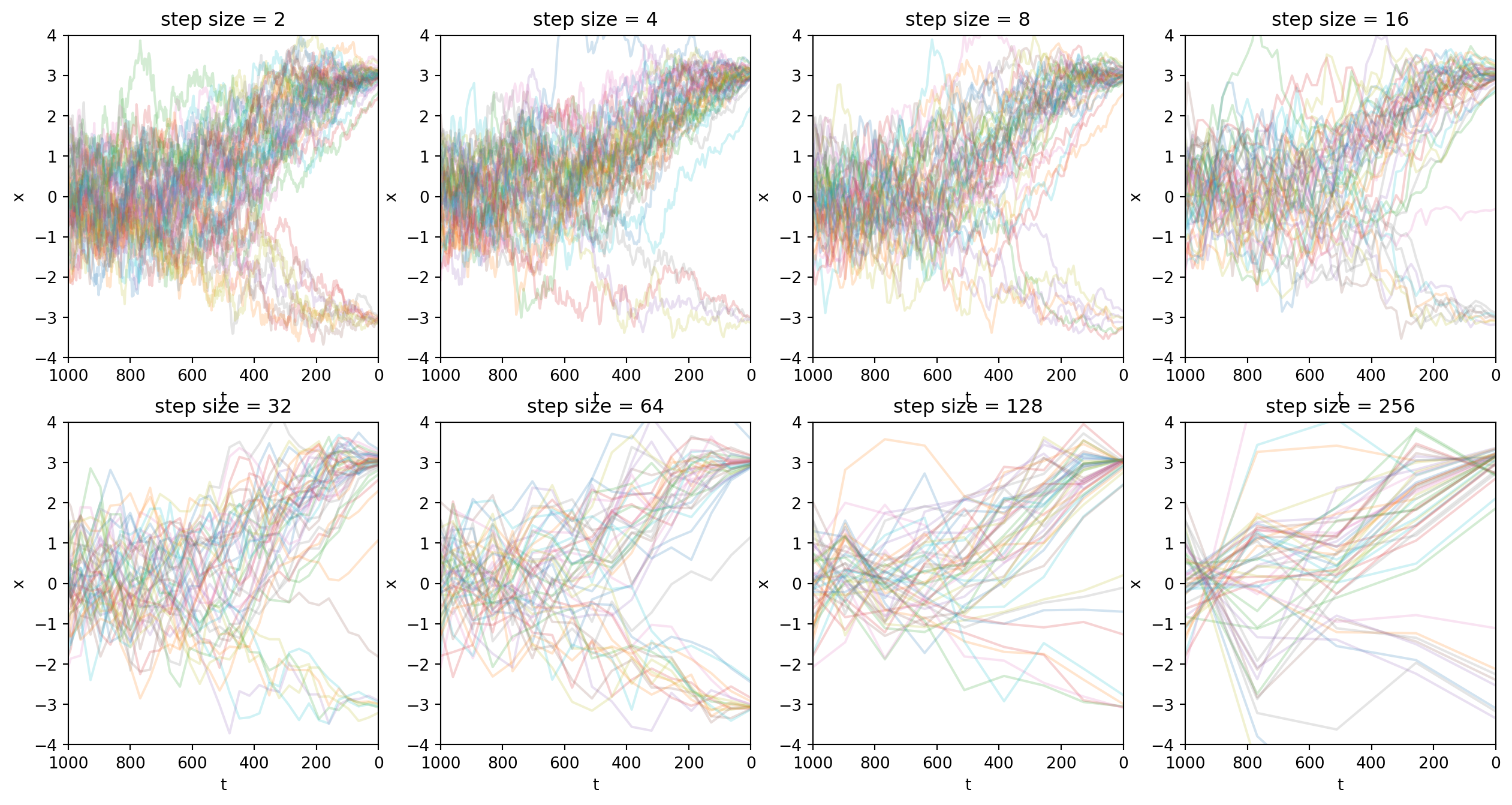
實驗結果顯示我們可以增加跳步幅度,成倍減小採樣開銷,同時採樣質量看起來還可以。
接下來的圖片展示了\(\sigma_t\)設為\(0\)這一特殊情況。可以看到,非常特別的:
- 採樣過程變得特別平滑,失去了隨機性。
- 採樣的終點強烈的由出發點決定。從某個latent出發,就一定會落在相近的某個採樣結果上。
- 這是一個優點:允許我們對latent進行插值。
- 相比之下,在DDPM中,從任意位置出發,終點的隨機性更強。對出發點的插值沒什麼意義。
繪圖代碼
plt.figure(figsize=(16, 8))
plt.subplot(241)
plot_denoise(1, sigma_style='ddim')
plt.subplot(242)
plot_denoise(2, sigma_style='ddim')
plt.subplot(243)
plot_denoise(4, sigma_style='ddim')
plt.subplot(244)
plot_denoise(8, sigma_style='ddim')
plt.subplot(245)
plot_denoise(16, sigma_style='ddim')
plt.subplot(246)
plot_denoise(32, sigma_style='ddim')
plt.subplot(247)
plot_denoise(64, sigma_style='ddim')
plt.subplot(248)
plot_denoise(128, sigma_style='ddim')
plt.show()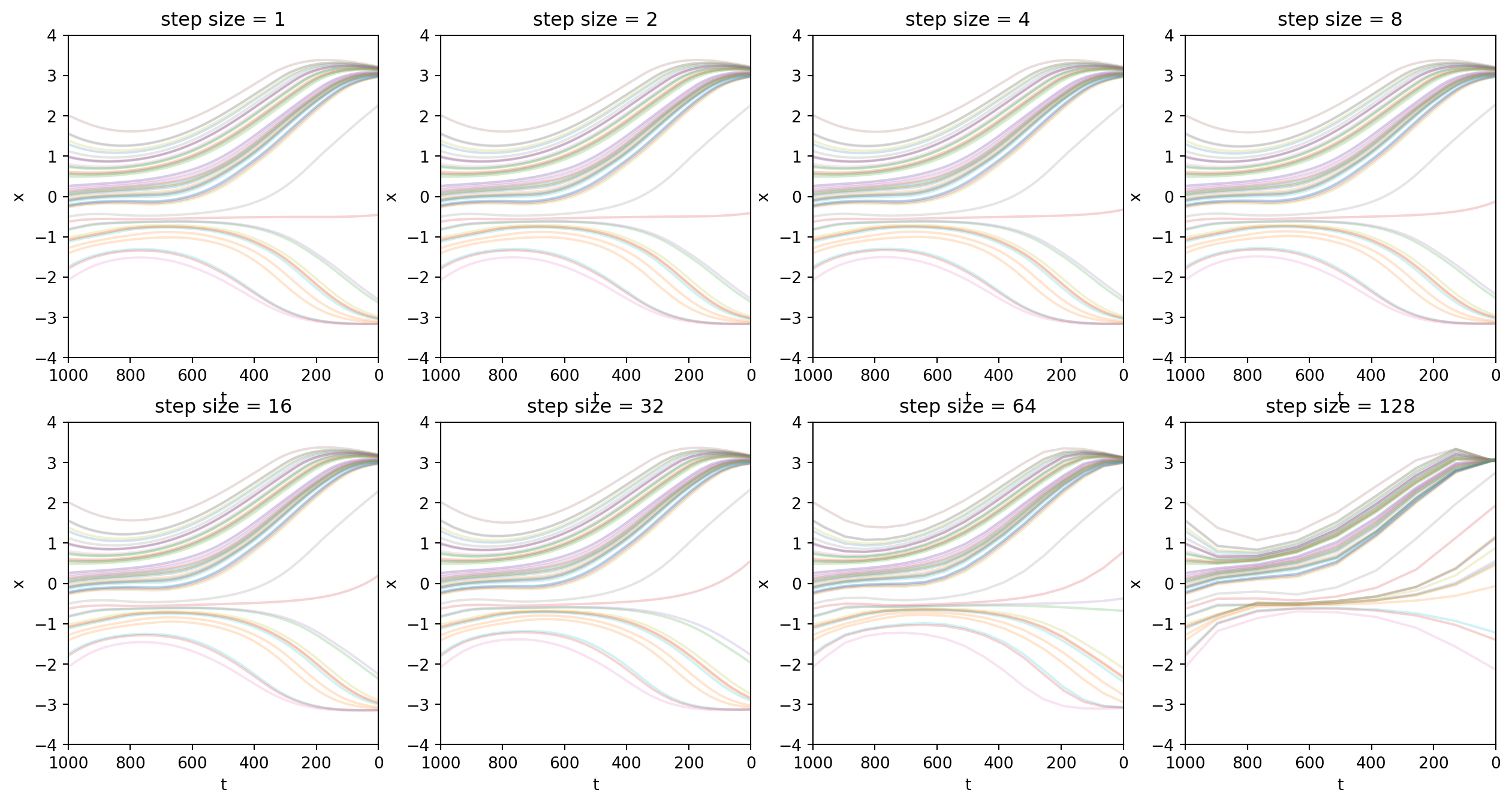
最後,我通過實驗驗證\(\sigma_t=0\)時,反向過程失去隨機性。從下面的圖片可以看到,參數一樣,不管採樣幾次,採樣軌跡都是相同的。
繪圖代碼
plt.figure(figsize=(16, 8))
plt.subplot(241)
plot_denoise(32, sigma_style='ddim')
plt.subplot(242)
plot_denoise(32, sigma_style='ddim')
plt.subplot(243)
plot_denoise(32, sigma_style='ddim')
plt.subplot(244)
plot_denoise(32, sigma_style='ddim')
plt.subplot(245)
plot_denoise(32, sigma_style='ddim')
plt.subplot(246)
plot_denoise(32, sigma_style='ddim')
plt.subplot(247)
plot_denoise(32, sigma_style='ddim')
plt.subplot(248)
plot_denoise(32, sigma_style='ddim')
plt.show()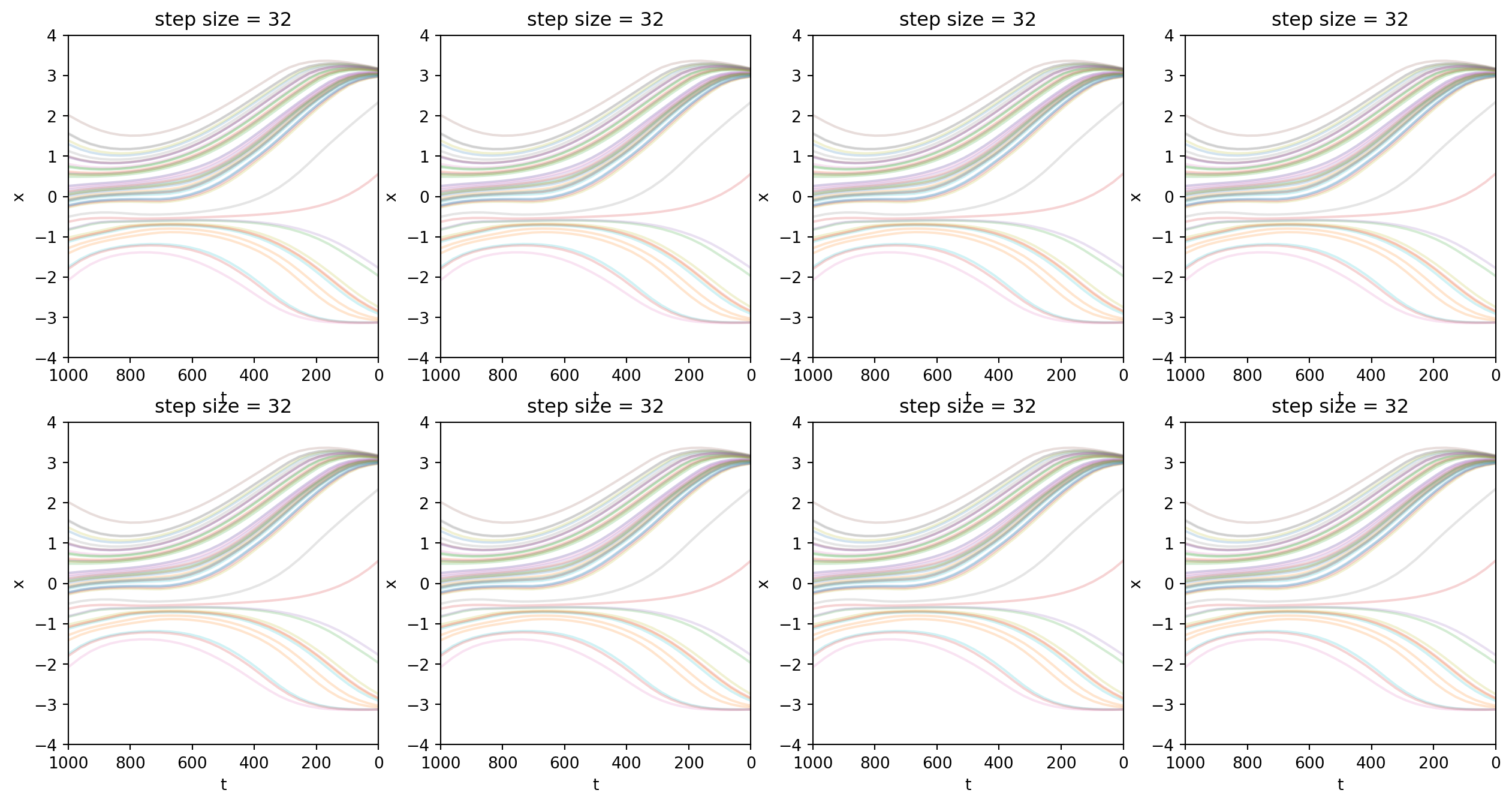
後記
本文介紹了DDPM和DDIM這兩篇重要的文章。文章裡面用簡單的離散型概率分佈作了簡單的演示和實驗,感覺結果比展示圖像生成模型直觀多了。而且運行也非常快。
費工夫寫完這篇文章,我自己的收穫也蠻多的😺擴散模型出來多年了,但我認為它們仍然值得啃一啃。
審美觀很重要。
過去我們已經見過許多風靡一時但是最終落伍的技術了。在技術迭代的進程裡面,怎麼找到那條主線,看見主題,就關係到審美能力的問題。
前段時間有人問我,「新的論文這麼多,怎麼才能看得過來?」我認為答案是「培養好自己的審美,只看你認為優美的工作。」因為若干年後回顧,我們將發現技術發展的主幹上,關鍵的工作就只有幾個。