最近在工作中用到了MinHash[1],使用它做了一些文档去重和查找相似数据的任务。工欲善其事,必先利其器。要想用好一个算法/工具,就需要深入了解它的底层细节。本文简单记录了我对MinHash方法的理解,并展示了一些简单的实验。
本文先介绍了将文档视为数字的集合这一思想,并演示了几种不同的实现方案;既然文章可以视为数的集合,那么自然可以用集合的交并比这一度量来衡量文章之间的相似度;接著,文章介绍了MinHash的核心:对集合的最小值进行采样,借此估测集合间的交并比;最后,文章介绍了MinHash作为一种局部敏感哈希(Locality Sensitive Hashing,LSH)具有怎样的特点,可以如何利用LSH的特点来加速文档去重过程。
在文章的开头,我们先罗列和导入后续会需要用到的包:
import numpy as np
import pandas as pd
from typing import Tuple, List, Set, Dict
from collections import defaultdict
import random
import time
import matplotlib.pyplot as plt
random.seed(0)1 将文档看作集合
文档可以看作是字符组成的序列。尽管现在使用RNN、Transformer等深度神经网络来处理文本的方法已经十分普遍,但当要处理文本规模达到上百万的量级时,忽略词语的语义、语序,仅考虑其词语构成,进行“机械的”相似度比较仍是一种有效的方法。
以文档A"a rose is a rose is a rose"和文档B"a rose is a flower which is a rose"为例,两个文档可以分别被拆解为如下的单词:
A = ("a", "rose", "is", "a", "rose", "is", "a", "rose")
B = ("a", "rose", "is", "a", "flower", "which", "is", "a", "rose")将A和B分别表示为其使用到的单词的集合是一种简单的方法。除此之外,还可以考虑将相邻的若干单词组成“Shingle”(又被称为n-gram),将文档考虑为Shingle的集合。
显然,Shingle可以被定义为字符串组成的n元组。
Shingle = Tuple[str]忽略Shingle的出现顺序,我们可以将文章看作是Shingle的集合。我们分普通集合和多重集两种情况分别讨论。
下面的代码展示了如何将一个文档转化为由Shingle构成的多重集。与普通的集合不同,多重集允许元素多次重复出现,这使得我们可以统计每种Shingle的出现次数。
代码使用Dict来模拟多重集。函数返回的Dict统计了文档中出现的每种Shingle的数量。
def doc_to_shingle_bag(doc: List[str], w:int) -> Dict[Shingle, int]:
assert w > 0, w
ret = defaultdict(int)
for i in range(len(doc) - w + 1):
ret[tuple(doc[i:i+w])] += 1
return ret
下面的代码展示了将文档A转化为Shingle的多重集的结果。Shingle的大小分别被设置为1、2、4.
print(doc_to_shingle_bag(A, 1))
print(doc_to_shingle_bag(A, 2))
print(doc_to_shingle_bag(A, 4))defaultdict(<class 'int'>, {('a',): 3, ('rose',): 3, ('is',): 2})
defaultdict(<class 'int'>, {('a', 'rose'): 3, ('rose', 'is'): 2, ('is', 'a'): 2})
defaultdict(<class 'int'>, {('a', 'rose', 'is', 'a'): 2, ('rose', 'is', 'a', 'rose'): 2, ('is', 'a', 'rose', 'is'): 1})其实不考虑Shingle的出现次数,将文档视为Shingle的普通集合也是可行的。这样的做法稍微粗糙一些,但效率更高。
doc_to_shingles函数提供了将文档转化为Shingle的集合的方法:
def doc_to_shingles(doc: List[str], w: int) -> Set[Shingle]:
assert w > 0, w
ret = set()
for i in range(len(doc) - w + 1):
ret.add(tuple(doc[i:i+w]))
return ret print(doc_to_shingles(A, 1))
print(doc_to_shingles(A, 2))
print(doc_to_shingles(A, 4)){('a',), ('rose',), ('is',)}
{('rose', 'is'), ('is', 'a'), ('a', 'rose')}
{('is', 'a', 'rose', 'is'), ('a', 'rose', 'is', 'a'), ('rose', 'is', 'a', 'rose')}MinHash方法[1]提出使用交并比(又被称为Jaccard相似度)来衡量文档间的相似度(resemblance)。交并比(即交集大小与并集大小之比)的计算公式如下:
\[ J(A, B) = \frac{|A\cap B|} {|A\cup B|} \]
如果文档被表示为多重集的话,我们可以使用下面的函数来计算其相似度:
def naive_resemblance_a(
shingles_a: defaultdict[Shingle, int],
shingles_b: defaultdict[Shingle, int]
) -> float:
i = 0
u = 0
for k in set(shingles_a.keys()) | set(shingles_b.keys()):
i += min(shingles_a[k], shingles_b[k])
u += max(shingles_a[k], shingles_b[k])
return i / max(u, 1e-6)下面的代码对相似度计算结果进行检查,可以看到计算结果与论文[1]提供的数据保持一致。
eps = 1e-6
ret = naive_resemblance_a(doc_to_shingle_bag(A, 1), doc_to_shingle_bag(B, 1))
assert abs(ret - 0.7) < eps, ret
ret = naive_resemblance_a(doc_to_shingle_bag(A, 2), doc_to_shingle_bag(B, 2))
assert abs(ret - 0.5) < eps, ret
ret = naive_resemblance_a(doc_to_shingle_bag(A, 3), doc_to_shingle_bag(B, 3))
assert abs(ret - 0.3) < eps, ret
print('All test cases passed.')All test cases passed.类似的,如下代码提供了将文档表示为Shingle的普通集合时,resemblance的计算方法,并作了检查:
def naive_resemblance_b(
shingles_a: Set[Shingle],
shingles_b: Set[Shingle]
) -> float:
intersection = shingles_a & shingles_b
union = shingles_a | shingles_b
return len(intersection) / max(len(union), 1e-6)eps = 1e-6
ret = naive_resemblance_b(doc_to_shingles(A, 1), doc_to_shingles(B, 1))
assert abs(ret - 0.6) < eps, ret
ret = naive_resemblance_b(doc_to_shingles(A, 2), doc_to_shingles(B, 2))
assert abs(ret - 0.5) < eps, ret
ret = naive_resemblance_b(doc_to_shingles(A, 3), doc_to_shingles(B, 3))
assert abs(ret - 0.42857142) < eps, ret
print('All test cases passed')All test cases passed将Shingle的大小记为\(w\),从以上的计算中我们可以看到\(w\)越大,resemblance就对差异越敏感。
至此,文章展示了如何将文档转化为Shingle的集合,并用交并比衡量文档相似性。在实际程序中,我们可以为每一种可能的Shingle分配一个id。至此,我们介绍了如何将文档表示为数字的集合。
上文介绍的方法与MinHash论文[1]保持一致。但这种方法仍是粗浅的。在实际的应用中,我们可以考虑是否去除stop words(即“a”, “the”,“of”等对文章语义贡献较小的词汇)。我们还可以考虑合并单词的不同形态,例如为“learn”、“learning”、“learned”赋予相同的id……除此之外,如何实现中文的分词也是一个值得深入的问题。本文就不再就此作更多探讨了。接下来,让我们假设文档已经被转化为数字的集合。
2 用最小值估计文档相似度
前文我们介绍了如何将文档表示为数字的集合,我们将这种操作记为\(S(A, w)\),其中\(A\)为输入的文档,\(w\)为shingle的尺寸。
在后面的文章中,我们可以生成一些随机集合用于实验(跳过shingle操作)。假设变量vocab_size规定了集合的最大尺寸,下面的代码能随机为我们生成一些“文章”:
vocab_size = 60000
def random_doc(k):
return set(random.sample(range(vocab_size), k))random_doc(4){25247, 49673, 55340, 58343}如前所述,文章的相似度可以用交并比(又名Jaccard similarity)衡量。既然文章被表示为集合,那么相似度的计算可以被实现为:
def Jaccard_similarity(doc_a, doc_b):
doc_a = set(doc_a)
doc_b = set(doc_b)
return len(doc_a & doc_b) / len(doc_a | doc_b)假设\(\Omega\)是所有可能的Shingle组成的集合。设\(\Omega\)是一个有序集,因此我们可以比较\(\Omega\)中所有元素的大小。对于\(\Omega\)的子集\(W\),定义 \[ \text{MIN}_s(W) = \left\{ \begin{aligned} &\text{W中最小的s个元素}, &\text{if} |W|\geq s \\ &W, &\text{otherwise} \end{aligned} \right., \] 定义 \[ M(A) = \text{MIN}_s(\pi(S(A, w))), \] 其中\(\pi:\Omega\rightarrow\Omega\)是定义在集合\(\Omega\)上的一个“置换”(即将\(\Omega\)集合作了一次“洗牌”,一一对应地将\(\Omega\)中的一个元素映射到另一个元素)。
那么:
定理 1 \[ \frac{|\text{MIN}_s(M(A)\cup M(B))\cap M(A) \cap M(B)|}{|\text{MIN}_s(M(A)\cup M(B)|} \tag{1}\] 是文档A和文档B的resemblance的无偏估计(以置换操作\(\pi\)是随机挑选的为前提)。
证明: 显然 \[ \begin{aligned} \text{MIN}_s(M(A)\cup M(B)) &= \text{MIN}_s(\pi(S(A, w))\cup \pi(S(B, w))) \\ &= \text{MIN}_s (\pi(S(A, w)\cup S(B, w))) \end{aligned} \] 设\(\alpha\)是\(\pi(S(A, w)\cup S(B, w))\)中最小的元素,那么 \[ \begin{aligned} P(\alpha \in M(A) \cap M(B)) &= P(\pi^{-1}(\alpha)\in S(A, w)\cap S(B, w)) \\ &= \frac{|S(A, w)\cap S(B, w)|}{|S(A, w)\cup S(B, w)|} \end{aligned} \] 假设\(\alpha\)是\(\pi(S(A, w)\cup S(B, w))\)中第二小、第三小……的元素,上式同样成立。因此命题成立。
这实际上是一个关于“超几何分布”的期望的问题,你可以在网络上查找相关讨论。
以上介绍的命题就是MinHash工作的核心原理。接下来,文章使用代码验证这个命题,并演示相关函数是如何工作的。
首先,我们先实现\(\text{MIN}_s\)函数:
def min_s(doc, s):
doc = np.asarray(list(doc))
return -find_top_k(-doc, s) \
if len(doc) > s \
else docmin_s的实现使用到了find_top_k函数。我隐藏了它的实现,实际上find_top_k是一个返回数组中最大的\(k\)个数的函数,可以用排序法或者quick select算法实现。
假设我们有一个大小为\(4\)的集合作为输入,那么min_s取\(s=2\)时的输出为:
d = random_doc(4)
print('document:', d)
print('min_s(document):', min_s(d, 2))document: {37120, 22297, 40130, 50311}
min_s(document): [37120 22297]MinHash中,随机性的来源是对置换操作\(\pi\)的采样。下面的代码随机初始化了一些候选的置换操作,可以作为\(\pi\)的候选。
random_permutations = []
for i in range(1000):
indices = list(range(vocab_size))
random.shuffle(indices)
random_permutations.append(indices)
random_permutation_index = 0def get_random_permutation():
global random_permutation_index
indices = random_permutations[random_permutation_index]
random_permutation_index += 1
random_permutation_index %= len(random_permutations)
pi = lambda x: [indices[i] for i in x]
return pi 接著实现\(M(A)\)函数。\(M(A) = \text{MIN}_s(\pi(S(A, w)))\),其代码实现为:
def m(pi, doc, s):
return min_s(pi(doc), s)利用min_s和m函数,resemblance计算的实现就直观明了了。根据公式 1,resemblance可以用如下代码估计:
def estimate_resemblance(pi, doc_a, doc_b, s):
ma = set(m(pi, doc_a, s))
mb = set(m(pi, doc_b, s))
tmp = set(min_s(ma | mb, s))
return len(tmp & ma & mb) / len(tmp) 下面的程序检验了estimate_resemblance函数对resemblance的估计结果与真值(Jaccard similarity)的一致性。实验表明MinHash所提出的方法确实能比较好地对Jaccard similarity进行估计。
errors = []
for i in range(8):
length_a = random.randint(10000, 30000)
length_b = random.randint(10000, 30000)
doc_a = random_doc(length_a)
doc_b = random_doc(length_b)
sim_j = Jaccard_similarity(doc_a, doc_b)
num_samples = 256
samples = []
for j in range(num_samples):
pi = get_random_permutation()
s = estimate_resemblance(pi, doc_a, doc_b, s=10)
samples.append(s)
resemblance_est = np.mean(samples)
# assert abs(sim_j - resemblance_est) < 1e-2
errors.append((sim_j - resemblance_est))
print('{}:{:.4f} ≈ {:.4f}'.format(i + 1, sim_j, resemblance_est))
print('Average error:', np.mean(np.abs(errors))) 1:0.2656 ≈ 0.2516
2:0.2224 ≈ 0.2391
3:0.1757 ≈ 0.1734
4:0.2111 ≈ 0.2066
5:0.2557 ≈ 0.2387
6:0.2848 ≈ 0.2785
7:0.1928 ≈ 0.1980
8:0.1944 ≈ 0.1961
Average error: 0.008473042802044726后续的方法[2]往往采用\(s=1\)的MinHash的特例。在\(s=1\)时,公式 1的含义就变为:
设\(A\)和\(B\)为待比较的输入文档,\(\pi\)为随机采样的置换。\(a=\min(\pi(A))\),\(b=\min(\pi(B))\),\(J(A, B) = P(a=b)\).
读者可以自行通过实验验证:当\(s=1\)时,MinHash也能很好地估计文档的相似度。
3 哈希函数
前文已经介绍了MinHash的核心思想,即基于随机采样的置换操作\(\pi\)选取最小的\(s\)个元素,根据这些元素是否相同,可以估计输入文档的相似度。但是随机置换\(\pi\)的生成比较耗时。考虑到shingle集合一般可以通过哈希函数\(h(\cdot)\)转化为范围有限的数字,然后这些数字经过置换操作\(\pi:\Omega\rightarrow\Omega\)在变换为\(\Omega\)内的其它数字,我们可以假设哈希函数\(h\)内部已经实现了置换操作,从而将\(\pi\)省略掉。这种假设的前提是\(h\)的哈希碰撞很少。
以下代码实现了一种哈希函数: \[ h_i(x) = (a_i x + b_i) \mod P \] ,其实现参考了chrisjmccormick的开源代码。
该哈希函数中,\(a_i\)和\(b_i\)分别是随机采样的系数,这使得哈希函数\(h_i\)具有随机性,对应于原\(\pi\)的随机性。
首先,我们需要随机选取\(a_i\)和\(b_i\),在代码中对应于coeff_a和coeff_b. 待要生成的哈希函数的数量记为num_hashes.
max_shingle_ID = 2**32-1
next_prime = 4294967311
num_hashes = 128
def pick_random_coeffs(k):
rand_list = []
for _ in range(k):
rand_index = random.randint(0, max_shingle_ID)
while rand_index in rand_list:
rand_index = random.randint(0, max_shingle_ID)
rand_list.append(rand_index)
return rand_list
coeff_a = pick_random_coeffs(num_hashes)
coeff_b = pick_random_coeffs(num_hashes)
print(coeff_a[:8], coeff_b[:8])[1725382162, 4099968420, 181011877, 2646584740, 2425745411, 1382556146, 2811366918, 584506969] [4024735497, 432468821, 4092063574, 1311785557, 3815225036, 3844735591, 2426666110, 66760331]那么,记录了num_hashes条随机哈希函数的列表可以实现为:
from functools import partial
hash_functions = [
partial(
lambda x, i: (coeff_a[i] * x + coeff_b[i]) % next_prime,
i=i
)
for i in range(num_hashes)
]以下是一些例子,说明不同的哈希函数对于同样的输入,输出是不同的:
hash_functions[0](0), hash_functions[1](0), hash_functions[0](0)(4024735497, 432468821, 4024735497)于是,对于输入文档doc,我们可以对应应用num_hashes条哈希函数,得到对应的哈希值作为它的“signature”。
def get_min_hash(doc):
hash_codes = [
min((hash_function(x) for x in doc))
for hash_function in hash_functions
]
return hash_codes 根据公式 1,signature的汉明距离(即数一数不同的哈希值的数量)就衡量了两篇文档的距离。让我们用实验来验证这一点:
random_docs = [random_doc(random.randint(10000, 30000)) for _ in range(8)]
hash_codes = [get_min_hash(doc) for doc in random_docs]
errors = []
total_time_j = 0
total_time_min_hash = 0
for i in range(len(random_docs)):
doc_a = random_docs[i]
min_hash_a = hash_codes[i]
for j in range(i + 1, len(random_docs)):
doc_b = random_docs[j]
min_hash_b = hash_codes[j]
t = time.time()
sim_j = Jaccard_similarity(doc_a, doc_b)
total_time_j += time.time() - t
t = time.time()
resemblance_est = np.mean([a == b for a, b in zip(min_hash_a, min_hash_b)])
total_time_min_hash += time.time() - t
errors.append((sim_j - resemblance_est))
print('{}-{}:{:.4f} ≈ {:.4f}'.format(i, j, sim_j, resemblance_est))
print('Average error:', np.mean(np.abs(errors)))
print('Time Difference: {:.4}s:{:.4}s'.format(total_time_j, total_time_min_hash))0-1:0.1899 ≈ 0.2031
0-2:0.1655 ≈ 0.1406
0-3:0.2121 ≈ 0.2812
0-4:0.1410 ≈ 0.1562
0-5:0.1861 ≈ 0.1094
0-6:0.1992 ≈ 0.1562
0-7:0.1130 ≈ 0.1250
1-2:0.1965 ≈ 0.1719
1-3:0.2701 ≈ 0.2812
1-4:0.1685 ≈ 0.1250
1-5:0.2263 ≈ 0.2188
1-6:0.2462 ≈ 0.2109
1-7:0.1313 ≈ 0.1406
2-3:0.2153 ≈ 0.2422
2-4:0.1431 ≈ 0.1328
2-5:0.1900 ≈ 0.1719
2-6:0.2063 ≈ 0.2109
2-7:0.1174 ≈ 0.1484
3-4:0.1840 ≈ 0.1328
3-5:0.2553 ≈ 0.2031
3-6:0.2885 ≈ 0.2188
3-7:0.1425 ≈ 0.1484
4-5:0.1633 ≈ 0.1406
4-6:0.1732 ≈ 0.1484
4-7:0.1084 ≈ 0.1250
5-6:0.2399 ≈ 0.1875
5-7:0.1304 ≈ 0.1953
6-7:0.1370 ≈ 0.1484
Average error: 0.03030614381569787
Time Difference: 0.1847s:0.09761s我们注意到该方法确实能大体反应文档间的Jaccard similarity。如果增大num_hashes,计算的结果可以变得更加准确。
此外,还可以看到比较signature的方法比直接计算Jaccard similarity要快上不少,这是因为signature的计算可以提前准备,而比较signature的汉明距离是很快的。
尽管将文档转化为Signature的方式加速了文档的两两比较,但这种方法的时间复杂度还是\(O(n^2)\). 面对海量的大规模数据,有没有能够避免两两比对的,快速找出相似数据的方法呢?
4 局部敏感哈希
如前所述,我们希望避免大量数据将两两比对的情况。已知每个文档都可以表示为一个由哈希值构成的列表,我们可以考虑两种简单的做法:
- 将所有哈希值完全一致的文档挑出来;
- 只要有一个任意位置,在列表的这个位置上哈希值重复,就将这些文档视为重复;
首先注意到这两种方法的时间复杂度都小于\(O(n^2)\),因为挑出哈希值重复的数据可以通过dict等数据结构实现;其次,这两种做法都是极端的。随着哈希函数数量的增加,1将挑不出任何数据,而2将返回所有数据——尽管如此,结合1和2,我们能得到一种折衷的,能实际应用的方案。
局部敏感哈希(Locality-Sensitive Hashing,LSH)就是这样一种,实现1和2的折中的技术。LSH方法首先要求相似的文档的哈希值有更大的概率相同,反之则希望它们大概率不同;其次,LSH方法将哈希函数分组,并鼓励相似的文档落入相同的bucket内。
接下来我们讨论哈希函数的分组。一组哈希函数被称为一个band。 设\(b\)为一个band内hash函数的数量,\(r\)为band的数量,于是使用到的哈希函数的总数为\(t=rb\). 那么对于随机选取的两个文档,它们的相似度为\(p\);那么在使用MinHash的前提下,其哈希值相同的概率也为\(p\)。有如下等式成立: \[ \begin{aligned} \text{一个band内所有哈希值都相同的概率} &= p^r \\ \text{一个band内存在不同哈希值的概率} &= 1 - p^r\\ \text{所有band都不相同的概率为} &= (1 - p^r)^b \\ \text{至少存在一个完全相同的band的概率为} &= f(p) = 1 - (1 - p^r)^b \\ \end{aligned} \] 将这个函数绘制出来,我们可以看到这样的图像:
t = 128
rb_list = [
[32, 4],
[16, 8],
[8, 16],
[4, 32],
]
plt.figure()
for r, b in rb_list:
assert r * b == t
p = np.linspace(0, 1, 1000)
fp = 1 - (1 - p**r)**b
plt.plot(p, fp)
plt.legend(['r={};b={}'.format(r, b) for r, b in rb_list])
plt.xlabel('p')
plt.ylabel('f(p)')
plt.show()
plt.close()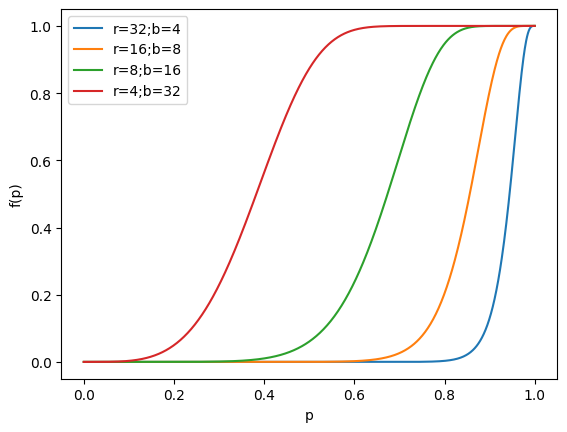
该函数的图像是一个递增的S形曲线。在\(p\)的值不超过某个阈值的时候,概率\(f(p)\)很小;反之一旦超过这个值,\(f(p)\)就骤然增大。
用通俗的话来说,MinHash方法具有一个很好的性质:相似的两个文档(\(p\)的值比较大)有很大的概率(\(f(p)\))使得至少存在一个band,这个band内的两文档的哈希值全部相同——这会使得它们落在同一个bucket内;函数图像中中部的跳变意味著存在一个可以调控的界限,在这个界限两端,文档落在同一bucket内的概率有鲜明的差别。
对于实际应用,该函数图像的“跳变点”是需要调控的一个重要参数。设我们希望提取相似度在阈值\(\tau\)以上的数据,那么上图的斜率最大点可以近似为\(\tau \approx (1/b)^{1/r}\),据此可以解出\(r,b\)的值。
5 总结
回想去年参与了一个大模型项目的数据管理,负责处理源数据,然后转给资源部标注。在这个项目里我没有料到供应商给的源数据居然有大量的重复,就这样把重复的数据发给资源部了……等到反应过来,已经不知道损失了多少钱。
_(¦3」∠)_
一开始用的是暴力的编辑距离或者TFIDF特征比较的方法去重,但随著数据的增多,两两比较的暴力去重开始变得有点应付不过来。后来才学习了基于哈希的去重方法。基于哈希的方法能有更高的效率,精准度高,召回率不如暴力方法。但是深入了解了算法细节,结合项目数据的特征,还是能够设计出好用的去重策略的。
6 一些参考资料
- MinHash Example
- MMDS text book
- http://www.mmds.org/