1 什麽是相機標定
影響相機成像過程的因素有很多。一束光先是從光源出發,落在物體表面。而後它又經過物體表面的反射,進入相機,穿過鏡頭和光圈,最後落在感光芯片上。這個過程中,物體的形狀、方位、焦距、光圈數、感光芯片的大小、感光單元的分佈間距……許許多多參數會對最終的成像產生影響。
相機標定是求解相機參數的過程。相機的參數又分為內參和外參。 内參包括相機的焦距、感光單元的間距、鏡頭畸變係數等。外參是相機相對於其它外部事物的位姿。一旦外參和内參是確定的,那我們就能確切地知道外部世界的某一個點發出的光綫會落在圖像的哪個位置。因此,許多任務,例如雙目視覺、增強現實、立體匹配、單目3D目標檢測……都需要使用準確的相機內外參。
內外參常常是無法直接精確測得的。我們無法直接用尺子測量鏡頭到感光芯片的距離,更無法用普通工具測量芯片上感光單元之間的間距(這是微米級別的尺寸),而鏡頭的畸變模型還帶來更多更複雜的因素。要如何精確地得出這些數值呢?
首先,我們要建立相機的數學模型。 本文介紹常見的針孔相機模型。它用小孔成像來近似相機的成像過程。理解針孔相機模型,有助於學習其它相機模型,例如魚眼相機模型和線陣相機模型。
相機模型建立後,我們用相機拍攝特定標定物,根據標定物的參數及成像效果,可以間接推斷出相機的各項參數。
2 相機坐標系和世界坐標系

常見的相機坐標系如圖 1所示。相機鏡頭朝前時,x軸朝右,y軸朝下,z軸朝前。
當然,你也可以採用不一樣的坐標系設定。坐標系的定義不同不會影響相機模型和參數標定過程的數學本質,標定的方法也是一樣的。但採取“另類”的設計有時會帶來一些不必要的麻煩。
與相機坐標系相對的是世界坐標系。世界坐标系的定义根据问题的不同而不同。它可以定义在某张标定板上,也可以定义在某个传感器上。某点世界坐标系与相机坐标系上的坐标可以通过刚性变换来转换。假设\(\mathbf p_w\)是世界坐标系下的坐标,\(\mathbf p_c\)是相机坐标系下的坐标,那么存在选择矩阵\(\mathbf R\)和平移向量\(\mathbf t\)使得 \[ \mathbf p_c= \mathbf R\mathbf p_w + \mathbf t \]
这里的向量\(\mathbf t=(t_x, t_y, t_z)^T\)。旋转矩阵\(\mathbf R\)是三行三列的方阵。
解释一下旋轉矩陣的計算。假設旋轉的過程是繞著z軸旋轉角度\(\gamma\),再繞y軸旋轉角度\(\beta\),再繞x軸旋轉角度\(\alpha\),那麼旋轉矩陣 \[ \mathbf R(\alpha, \beta, \gamma) = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right) \left(\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right) \left(\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0\\ \sin \gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{array}\right). \]
所以,旋轉矩陣可以由3個旋轉角度決定。這三個角度被稱為歐拉角。
需要注意,旋轉角度、旋轉軸的順序不是唯一的。比如,也可以先繞\(x\)軸旋轉一個角度,再繞\(z\)軸旋轉,再繞\(x\)軸旋轉。在具體的問題中,要注意歐拉角的定義。
總而言之,六元組\((t_x, t_y, t_z, \alpha, \beta, \gamma)\)決定了參考坐標系,它們構成相機的外參。
3 針孔相機模型
3.1 透視投影
接下來介紹針孔相機模型。
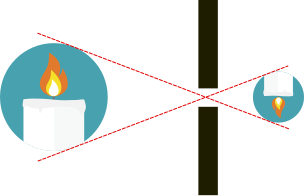
我們忽略光線所具有的“波”的性質。我們僅需知道,“光是沿直線傳播的”。那麼,如圖 2所示物體上發出的光只能經過小孔落在成像平面上。經過小孔,上方的光綫落在下面,下方的光綫落在上面。小孔成像所成的是倒立的實像。
雖然小孔成像在物理上是這樣解釋的,但是,計算機從業者卻常用另外的圖示來表達這一過程。
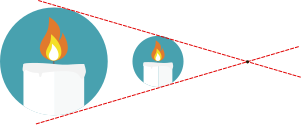
在圖 3中,你可以看到對象物體和所成像都畫在小孔(又被稱爲主点)的同一側,並且直接繪製正像。你可能會問,這種事在物理上怎麽可能發生呢?
這在物理上當然是不合理的。之所以計算機的從業者這樣繪圖,只是因爲方便。這種畫法因爲能節省作圖空間,且避免了麻煩的坐標系旋轉而十分常見。通過避免坐標旋轉,可以簡化數學運算。
小孔成像的原理可以很容易用數學公式描述。假設相機坐標系中有一點\(\mathbf p_c=(x_c, y_c, z_c)^T\),這個點發出的光綫經過了小孔,那麽可以通過如下公式求得成像點的位置:
\[ x = \frac{x_c f}{z_c}, y = \frac{y_c f}{z_c}.\]
其中\(f\)是小孔到成像平面的距離。 圖 4或許有助於你理解該公式。從圖中我們可以看到,成像點總是位於\(z = f\)的平面上,並且與原點\(\mathbf o\)和被成像點\(\mathbf p_c\)共線。因此,我們只須求出直線\(\mathbf o \mathbf p_c\)與成像平面的角點,也就得到了成像點的坐標。
在計算機視覺應用中,圖像會被離散化為以像素為單位的矩陣。要將\(x\)和\(y\)坐標同像素的行列對應起來,還需要在成像公式中加入縮放係數和偏移量:
\[ c = \frac{x_c f}{z_c s_x} + c_x, r = \frac{y_c f}{z_c s_y} + c_y. \]
這裏\(s_x\)和\(s_y\)就是感光芯片陣列在橫向和縱向上的間距。 這樣,通過這個公式,我們就知道點\(\mathbf p_c\)落在圖像\(r\)行\(c\)列的位置。
令\(f_x = f / s_x\),以及\(f_y = f / s_y\),則有
\[ c = \frac{x_c f_x}{z_c} + c_x, r = \frac{y_c f_y}{z_c} + c_y.\]
對於市面上的相機,一般都有\(s_x=s_y\),於是\(f_x = f_y\)。一種\(s_x\neq s_y\)的特殊情況(見文獻[1] 71頁的2.3.1節),是採集卡的時鐘頻率與攝像機時鐘頻率不一致從而導致像素橫縱比率改變。這種情形比較少見。
這兩個公式可以轉寫為方便的矩陣乘法的形式: \[ (c',r', z_c)^T = \left( \begin{array}{ccc} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x_c\\ y_c\\ z_c \\ \end{array} \right) = \mathbf P \left( \begin{array}{c} x_c\\ y_c\\ z_c \\ \end{array} \right) \] 其中\(\mathbf P\)被稱為投影矩陣,\(c'\)、\(r'\)是橫縱坐標的分子,而\(z_c\)是它們公共的分母: \[ c = \frac{c'}{z_c} \]
\[ r = \frac{r'}{z_c} \]
結合內參和外參,則成像點的計算公式是: \[ s\left( \begin{array}{c} c\\r\\1 \end{array} \right) = \mathbf P(\mathbf R\mathbf p_w + \mathbf T) = \mathbf P (\mathbf r_1, \mathbf r_2, \mathbf r_3, \mathbf t) \left( \begin{array}{c} x_w\\ y_w\\ z_w\\ 1 \end{array} \right) \tag{1}\] 其中\(r_i\)是矩陣\(\mathbf R\)的第i列。
3.2 鏡頭畸變
對於大多數鏡頭而言,它們的畸變都可以被近似為徑向畸變。

徑向畸變: \[ \left( \begin{array}{c} u' \\ v' \end{array} \right) = \frac{2}{1 + \sqrt{1 - 4 \kappa (u^2 + v^2)}} \left( \begin{array}{c} u \\ v \end{array} \right) \]
這是Halcon庫採用的畸變公式。不同的程序庫或文獻可能使用不同的畸變公式。例如,OpenCV有一套更複雜的畸變描述方式。 它們的共同特征是用非線性函數來表示畸變。
昂貴的工業相機可以使用簡單的畸變模型,而便宜的網絡相機可能需要使用複雜的畸變模型。
4 標定
標定就是求解相機內外參的過程。對於針孔相機模型,我們有內參數\((\kappa, f_x, f_y, c_x, c_y)\),外參數\((\alpha, \beta, \gamma, t_x, t_y, t_z)\). 標定時我們需要拍攝多張標定板的圖像。雖然相機的內參是固定的,但每次拍攝,標定板的位置都不一樣,所以每次拍攝都產生一組待解的外參。總的待解參數的量是\(\text{內參數量}+\text{外參數量}\times\text{圖片數量}\).
4.1 標定工具
我們使用張氏標定法來完成標定。需要使用標定板這一工具

標定板是黑白相間的方格子,這種被稱為“棋盤格標定板”。材質有A4紙的、鋁合金的,也有玻璃制的。材質決定了標定板的精度,也影響標定精度。如果你的應用場景對標定精度的要求很高,你可能需要選擇一種昂貴的材料,而不是簡單地用A4紙打印一張標定板。
我們檢測的是棋盤格標定板上的角點。角點的個數最好是奇數個x偶數個。圖案最好不是旋轉對稱的。
也有圓形圖案的標定板。但我更喜歡棋盤格圖案,因為圓形的投影中心不一定是圓形的中心,這會給檢測帶來麻煩。另外,角點檢測也比邊緣檢測準確,後者容易受光照影響而發生偏移。橢圓擬合的準確性依賴於邊緣檢測,因此拍照時必須控制好光照。
4.2 標定流程
標定時,我們從多個方位拍攝標定板,產生若干圖像(例如15張,30張)。
拍好照片後,可以使用廣為人知、影響深遠的張氏標定法[2]求解相機內外參。
4.3 內外參的閉式解
先從簡單的情況著手——假設不存在畸變,此時問題有閉式解。
我們需要做的只是求解線性變換:
\[ s\left( \begin{array}{c} c\\r\\1 \end{array} \right) = \mathbf P(\mathbf R\mathbf p_w + \mathbf T) = P (\mathbf r_1, \mathbf r_2, \mathbf r_3, \mathbf t) \left( \begin{array}{c} x_w\\ y_w\\ z_w\\ 1 \end{array} \right) \]
注意標定板是平面,所以\(z_w = 0\),上式化簡為
\[ s\left( \begin{array}{c} c\\r\\1 \end{array} \right) = \mathbf P(\mathbf R\mathbf p_w + \mathbf T) = \mathbf P (\mathbf r_1, \mathbf r_2, \mathbf t) \left( \begin{array}{c} x_w\\ y_w\\ 1 \end{array} \right) \]
令\(\mathbf H = \mathbf P(\mathbf r_1, \mathbf r_2 , \mathbf t)\),上式可以寫為 \[\tilde{\mathbf m} = \mathbf H \tilde{\mathbf M}\] 其中\(\tilde{\mathbf m}\)表示點在圖像上的投影的齊次坐標,\(\tilde{\mathbf M}\)表示點在標定板上的坐標。 只要標定板上的點足夠多,那麼就可以用最小二乘法求得\(\mathbf H\).
又令\(\mathbf H = \left[\mathbf h_1, \mathbf h_2, \mathbf h_3\right]\),其中\(\mathbf h_i\)是其第i列的三維向量。
由於R是單位正交陣,所以\(r_1\), \(r_2\)是相互正交的單位向量,故而 \[ \mathbf h_1^T \mathbf P^{-T} \mathbf P^{-1} \mathbf h_2 = 0 \tag{2}\]
\[ \mathbf h_1^T \mathbf P^{-T} \mathbf P^{-1} \mathbf h_1 = \mathbf h_2^T \mathbf P^{-T} \mathbf P^{-1} \mathbf h_2 \tag{3}\]
再令 \[\mathbf B = \lambda \mathbf P^{-T} \mathbf P^{-1} \equiv \left( \begin{array}{ccc} B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22} & B_{23} \\ B_{13} & B_{23} & B_{33} \\ \end{array}\right) \] 其中\(\lambda\)是一個任意的縮放係數。\(\mathbf B\)是一個對稱矩陣。注意到由於本文對\(\mathbf P\)的定義,\(B_{12}=0\). 所以\(\mathbf B\)可以由六維向量\(\mathbf b = \left(B_{11}, B_{22}, B_{13}, B_{23}, B_{33}\right)^T\)決定。
設\(\mathbf h_i = (h_{i1}, h_{i2}, h_{i3})^T\)是\(\mathbf H\)的第i列,那麼, \[ \mathbf h_i^T \mathbf{B} \mathbf h_j = \mathbf v_{ij}^T \mathbf b, \] 其中 \[ \mathbf v_{ij} = (h_{i1}h_{j1}, h_{i2}h_{j2}, h_{i3}h_{j1} + h_{i1} h _{j3}, h_{i3}h_{j2} + h_{i2}h_{j3}, h_{i3}h_{j3}) \] 於是,公式 2、公式 3中的約束可以轉化為如下線性約束: \[ \left(\begin{array}{c} \mathbf v_{12}^T \\ (\mathbf v_{11} - \mathbf v_{12}) ^T \end{array} \right) \mathbf b = \mathbf 0 \]
假設我們拍攝了n張圖片,那麼將n個這樣的公式堆疊起來,就得到 \[ \mathbf V \mathbf b = \mathbf 0 \]
\(\mathbf V\)是由\(\mathbf H\)決定的,可以通過單張圖像求得,而\(\mathbf b\)是由相機的內參決定的。我們要求得\(\mathbf b\)。可以用著名的線性最小二乘法求解這個問題。只要數據點足夠多,則這個問題有閉式解。
一旦\(\mathbf b\)得解,那麼我們可以恢復出相機的內參。可以證明 \[ \begin{aligned} c_y &= - B_{11} B_{23} / (B_{11}B_{22}) \\ \lambda &= B_{33} - (B_{13}^2 + c_y (- B_{11}B_{23})) / B_{11} \\ f_x &= \sqrt{\lambda / B_{11}} \\ f_y &= \sqrt{\lambda B_{11} / (B_{11}B_{22})} \\ c_x &= - B_{13} \alpha^2 / \lambda \end{aligned} \]
接下來,各張圖像的外參也可依次求得。 \[ \mathbf r_1 = \lambda \mathbf A^{-1}\mathbf h_1, \mathbf r_2 = \lambda \mathbf A^{-1} \mathbf h_2 , \mathbf r_3 = \mathbf r_1 \times \mathbf r_2, \mathbf t = \lambda \mathbf A ^{-1} \mathbf h_3\] 注意,這裡求解出的旋轉矩陣可能不是單位正交矩陣,需要用SVD分解的方法將其轉變為單位正交陣。
總結一下本小節的內容:假設相機沒有畸變,那麼可以先求得每張圖像對應的單應性變換矩陣\(\mathbf H\),然後,可以依次求得相機內外參。這種情況下,內外參數的解是閉式解。
4.4 求相機的畸變係數
上一節,我們求解了相機的內外參。但這種解法存在幾個問題:
- 我們假設相機沒有畸變;
- 我們通過最小二乘來求解問題。但這裡應用的最小二乘所最小化的距離度量沒有實際的物理意義。
所以,張氏標定法用上一節所介紹的方法求得的解作為初始解,用LM算法繼續優化該解。目標函數為: \[\sum_{i} \sum_{j} \left\| m_{ij} - \phi(\mathbf P, \mathbf R_i \mathbf t_i, \mathbf M_j)\right\| ^2\] 其中\(\phi\)是考慮了相機畸變的非線性投影函數,解決了問題 1. 新的目標函數旨在最小化投影誤差,是具有實際物理意義的,解決了問題2.
5 思考題
一張標定板最少應該有多少個點?至少應當拍攝多少張標定板圖像?
標定板的點數至少應該使得\(H\)可解。而三維方陣\(H\)作為單應性變換,有8個自由度。 標定板的每個點都可以提供兩行投影方程,因此如果有四個點,則理論上\(H\)可解。因為\(\mathbf V\)是\(2n\)行的矩陣,而內參(不包括畸變係數,分別是\(f_x\)、\(f_y\)、\(c_x\)、\(c_y\))有4個,故而理論上圖片張數\(n\geq 2\)時問題可解。
當然,實際上為了獲得較好的精度,我們會適當取多一些點,多幾張圖片。實踐中,如果點數、圖片數不夠多,解的精度是很差的。
6 參考文獻
7 附錄
7.1 標定算法的Python實現
OpenCV/Halcon等庫提供了標定用的函數,可以非常方便的用Python或者C++調用。儘管如此,不同的程序庫使用的相機模型有略微的差別。只有真正了解相機模型,理解每一個參數,才能正確地使用它們。
參考Halcon的資料[1] ,我用Python實現了一份標定算法。經測試,標定結果同Halcon的標定算法所產生的結果一致(誤差小於0.01)。這份代碼對於理解Halcon的相機模型、標定原理可能有幫助,僅供參考。
展開代碼
# -*- coding: utf-8 -*-
import numpy as np
import cv2 as cv
sin, cos = np.sin, np.cos
# 旋转矩阵分解为欧拉角
# 该函数只能得到其中一种特解
# 参考:https://www.geometrictools.com/Documentation/EulerAngles.pdf
def rotate_matrix_factorize(mat):
assert(mat.shape == (3, 3))
eps = np.finfo(mat.dtype).eps
r00, r01, r02, r10, r11, r12, r20, r21, r22 = mat.flatten()
if np.abs(r02 - 1) < eps:
# 标定板正好垂直于成像平面,
# 分解方式不唯一,
# 随便返回一个特解算了
return 0, np.pi / 2, np.arctan2(r10, r11)
# TODO: 把这种标定板剔除掉比较好
elif np.abs(r01 + 1) < eps:
# 如同上一种情况
return 0, -np.pi / 2, np.arctan2(r10, r11)
else:
return np.arctan2(-r12, r22), np.arcsin(r02), np.arctan2(-r01, r00)
# 由投影变换矩阵和内参估计外参
def estimate_outer_params(cx, cy, fx, fy, mat_h):
# 内参矩阵
mat_m = np.matrix([[fx, 0, cx],
[0, fy, cy],
[0, 0, 1]])
lamb = 1 / np.linalg.norm(np.matmul(mat_m.I, mat_h[:, 0]))
# 旋转矩阵
r1 = lamb * np.matmul(mat_m.I, mat_h[:, 0])
r2 = lamb * np.matmul(mat_m.I, mat_h[:, 1])
r3 = np.cross(r1, r2)
mat_r = np.array([r1, r2, r3]).reshape((3, 3)).T
# 旋转矩阵要强制转化为正交的
u, s, vh = np.linalg.svd(mat_r)
mat_r = np.matmul(np.matmul(u, np.eye(3, 3)), vh)
# 从旋转矩阵取旋转角度
alpha, beta, gamma = rotate_matrix_factorize(mat_r)
# 位移向量
t = np.array(lamb * np.matmul(mat_m.I, mat_h[:, 2].reshape(3, 1)))
return alpha, beta, gamma, t
def predict1(points, cx, cy, sx, sy, f, kappa, outer_params):
scene_num = outer_params.shape[0]
pt_num = points.shape[0]
assert(outer_params.shape == (scene_num, 6))
assert(points.shape == (pt_num, 2))
points_transpose = points.T # shape: (2, pt_num)
points_camera = np.empty((3, pt_num * scene_num))
# 变换到相机坐标系
for i in range(scene_num):
alpha, beta, gamma, tx, ty, tz = outer_params[i]
# 绕z轴旋转。
points_rotate_z = np.matmul([
[np.cos(gamma), -np.sin(gamma)],
[np.sin(gamma), np.cos(gamma)]
],
points_transpose)
assert(points_rotate_z.shape == (2, pt_num))
# 绕y轴旋转
points_rotate_y = np.matmul([
[np.cos(beta), 0],
[0, 1],
[-np.sin(beta), 0]
],
points_rotate_z)
assert(points_rotate_y.shape == (3, pt_num))
# 绕x轴旋转
points_rotate_x = np.matmul([
[1, 0, 0],
[0, np.cos(alpha), -np.sin(alpha)],
[0, np.sin(alpha), np.cos(alpha)]
], points_rotate_y)
# 平移到相机坐标系
points_camera[:, i * pt_num: (i + 1) * pt_num] = points_rotate_x + [[tx], [ty], [tz]]
# 投影到成像平面
points_image_plane = points_camera[:2, :] / points_camera[2, :] * f
assert(points_image_plane.shape == (2, pt_num * scene_num))
# 畸变
r2 = np.sum(np.power(points_image_plane, 2), axis=0)
assert(r2.shape == (pt_num * scene_num,))
ratio = 2 / (1 + np.sqrt(1 - 4 * kappa * r2))
points_distort = ratio * points_image_plane
assert(points_distort.shape == (2, pt_num * scene_num))
r2d = np.sum(np.power(points_distort, 2), axis=0)
assert(r2d.shape == (pt_num * scene_num,))
# 到图像坐标系
points_image = [[1 / sx], [1 / sy]] * points_distort + [[cx], [cy]]
assert(points_image.shape == (2, pt_num * scene_num))
# 雅可比矩阵,左起5列对应内参cx, cy, sx, f, kappa,往右每6列对应一组外参
# 上半部分对应标定点的横坐标,下半部分对应纵坐标
jac = np.empty((2 * pt_num * scene_num, 5 + scene_num * 6))
# 横坐标对cx的偏导数
jac[:pt_num * scene_num, 0] = 1
# 纵坐标对cx的偏导数
jac[pt_num * scene_num:, 0] = 0
# 对cy的偏导数
jac[:pt_num * scene_num, 1] = 0
jac[pt_num * scene_num:, 1] = 1
# 对sx的偏导数
jac[:pt_num * scene_num, 2] = -points_distort[0, :] / sx ** 2
jac[pt_num * scene_num:, 2] = 0
# 对f求偏导数
d_ud_u = 2 * kappa * points_distort[0, :] ** 2 / np.sqrt(1 - 4 * kappa * r2) + ratio
d_ud_v = 2 * kappa * points_image_plane[0, :] * points_distort[1, :] ** 2 / points_image_plane[1, :] / np.sqrt(1 - 4 * kappa * r2)
d_vd_u = d_ud_v
d_vd_v = 2 * kappa * points_distort[1, :] ** 2 / np.sqrt(1 - 4 * kappa * r2) + ratio
jac[:pt_num * scene_num, 3] = (1 / sx * (d_ud_u * points_camera[0, :] / points_camera[2, :]
+ d_ud_v * points_camera[1, :] / points_camera[2, :])).flatten()
jac[pt_num * scene_num:, 3] = (1 / sy * (d_vd_u * points_camera[0, :] / points_camera[2, :]
+ d_vd_v * points_camera[1, :] / points_camera[2, :])).flatten()
# 对kappa的偏导数
jac[:pt_num * scene_num, 4] = (1 / sx * points_image_plane[0] / np.sqrt(1 - 4 * kappa * r2) * r2d).flatten()
jac[pt_num * scene_num:, 4] = (1 / sy * points_image_plane[1] / np.sqrt(1 - 4 * kappa * r2) * r2d).flatten()
# 对外参求偏导数
# shape: (pt_num * scene_num,)
d_c_xc = 1 / sx * d_ud_u * f / points_camera[2, :]
d_c_yc = 1 / sx * d_ud_v * f / points_camera[2, :]
d_c_zc = -1 / sx * (d_ud_u * f * points_camera[0, :] / points_camera[2, :] ** 2
+ d_ud_v * f * points_camera[1, :] / points_camera[2, :] ** 2)
d_r_xc = 1 / sy * d_vd_u * f / points_camera[2, :]
d_r_yc = 1 / sy * d_vd_v * f / points_camera[2, :]
d_r_zc = -1 / sy * (d_vd_u * f * points_camera[0, :] / points_camera[2, :] ** 2
+ d_vd_v * f * points_camera[1, :] / points_camera[2, :] ** 2)
for scene in range(scene_num):
d_c_xc_slice = d_c_xc[scene * pt_num:(scene + 1) * pt_num]
d_c_yc_slice = d_c_yc[scene * pt_num:(scene + 1) * pt_num]
d_c_zc_slice = d_c_zc[scene * pt_num:(scene + 1) * pt_num]
d_r_xc_slice = d_r_xc[scene * pt_num:(scene + 1) * pt_num]
d_r_yc_slice = d_r_yc[scene * pt_num:(scene + 1) * pt_num]
d_r_zc_slice = d_r_zc[scene * pt_num:(scene + 1) * pt_num]
jac_slice1 = jac[scene * pt_num:(scene + 1) * pt_num, :]
jac_slice2 = jac[(scene_num + scene) * pt_num:(scene_num + scene + 1) * pt_num, :]
alpha, beta, gamma, _, _, _ = outer_params[scene]
# xc = [cos(beta) * cos(gamma) * x - cos(beta) * sin(gamma) * y],
# yc = [x * (cos(alpha) * sin(gamma) + cos(gamma) * sin(alpha) * sin(beta))
# + y * (cos(alpha) * cos(gamma) - sin(alpha) * sin(beta) * sin(gamma))],
# zc = [x * (-cos(alpha) * cos(gamma) * sin(beta) + sin(alpha) * sin(gamma))
# + y * (cos(alpha) * sin(beta) * sin(gamma) + cos(gamma) * sin(alpha))]
d_xc_alpha = 0
d_xc_beta = -sin(beta) * cos(gamma) * points_transpose[0, :] \
+ sin(beta) * sin(gamma) * points_transpose[1, :]
d_xc_gamma = -cos(beta) * sin(gamma) * points_transpose[0, :] \
- cos(beta) * cos(gamma) * points_transpose[1, :]
d_yc_alpha = points_transpose[0, :] * (-sin(alpha) * sin(gamma) + cos(gamma) * cos(alpha) * sin(beta)) \
+ points_transpose[1, :] * (-sin(alpha) * cos(gamma) - cos(alpha) * sin(beta) * sin(gamma))
d_yc_beta = points_transpose[0, :] * cos(gamma) * sin(alpha) * cos(beta) \
- points_transpose[1, :] * sin(alpha) * cos(beta) * sin(gamma)
d_yc_gamma = points_transpose[0, :] * (cos(alpha) * cos(gamma) - sin(gamma) * sin(alpha) * sin(beta)) \
+ points_transpose[1, :] * (-cos(alpha) * sin(gamma) - sin(alpha) * sin(beta) * cos(gamma))
d_zc_alpha = points_transpose[0, :] * (sin(alpha) * cos(gamma) * sin(beta) + cos(alpha) * sin(gamma)) \
+ points_transpose[1, :] * (-sin(alpha) * sin(beta) * sin(gamma) + cos(gamma) * cos(alpha))
d_zc_beta = points_transpose[0, :] * -cos(alpha) * cos(gamma) * cos(beta) \
+ points_transpose[1, :] * cos(alpha) * cos(beta) * sin(gamma)
d_zc_gamma = points_transpose[0, :] * (cos(alpha) * sin(gamma) * sin(beta) + sin(alpha) * cos(gamma)) \
+ points_transpose[1, :] * (cos(alpha) * sin(beta) * cos(gamma) - sin(gamma) * sin(alpha))
# alpha
jac_slice1[:, 5 + scene * 6] = d_c_xc_slice * d_xc_alpha + d_c_yc_slice * d_yc_alpha + d_c_zc_slice * d_zc_alpha
jac_slice2[:, 5 + scene * 6] = d_r_xc_slice * d_xc_alpha + d_r_yc_slice * d_yc_alpha + d_r_zc_slice * d_zc_alpha
# beta
jac_slice1[:, 6 + scene * 6] = d_c_xc_slice * d_xc_beta + d_c_yc_slice * d_yc_beta + d_c_zc_slice * d_zc_beta
jac_slice2[:, 6 + scene * 6] = d_r_xc_slice * d_xc_beta + d_r_yc_slice * d_yc_beta + d_r_zc_slice * d_zc_beta
# gamma
jac_slice1[:, 7 + scene * 6] = d_c_xc_slice * d_xc_gamma + d_c_yc_slice * d_yc_gamma + d_c_zc_slice * d_zc_gamma
jac_slice2[:, 7 + scene * 6] = d_r_xc_slice * d_xc_gamma + d_r_yc_slice * d_yc_gamma + d_r_zc_slice * d_zc_gamma
# tx
jac_slice1[:, 8 + scene * 6] = d_c_xc_slice
jac_slice2[:, 8 + scene * 6] = d_r_xc_slice
# ty
jac_slice1[:, 9 + scene * 6] = d_c_yc_slice
jac_slice2[:, 9 + scene * 6] = d_r_yc_slice
# tz
jac_slice1[:, 10 + scene * 6] = d_c_zc_slice
jac_slice2[:, 10 + scene * 6] = d_r_zc_slice
return points_image, jac
def calibrate(grids, params):
pattern_size = params['pattern size']
cell_width = params['cell width']
image_count = grids.shape[0]
# 随机显示一张标定板检测结果
# import random
# show_grid(pattern_size, imgs, grids, random.randint(0, len(imgs) - 1))
# 计算世界坐标系中的标定板坐标
grid_x = (np.arange(pattern_size[0] * pattern_size[1]) % pattern_size[0]) * cell_width
grid_y = np.asarray(np.arange(pattern_size[0] * pattern_size[1]) / pattern_size[0], np.int) * cell_width
grid_world = np.empty((pattern_size[0] * pattern_size[1], 2))
grid_world[:, 0] = grid_x
grid_world[:, 1] = grid_y
# 提取内参初始值
obj_points = np.float32(np.tile(np.hstack((grid_world, np.zeros((grid_world.shape[0], 1)))), (image_count, 1)))\
.reshape(image_count, pattern_size[0] * pattern_size[1], 3)
camera_matrix = np.array(cv.initCameraMatrix2D(
obj_points,
np.float32(grids),
(1280, 1024)
))
fx, _, cx, _, fy, cy, _, _, _ = camera_matrix.flatten()
sy = 4.8e-3
f = fy * sy
sx = f / fx
kappa = 0
outer_params = np.empty((image_count, 6))
for i in range(image_count):
mat_h, _ = cv.findHomography(obj_points[i], grids[i])
alpha, beta, gamma, t = estimate_outer_params(cx, cy, f / sx, f / sy, mat_h)
outer_params[i, :] = [alpha, beta, gamma, t[0], t[1], t[2]]
lamb = 100
g1 = 0.1
g2 = 1.1
i1 = 1e-1
i2 = 0.99
mat_i = np.eye(5 + 6 * image_count)
for i in range(100):
points_predict, jac = predict1(grid_world, cx, cy, sx, sy, f, kappa, outer_params)
assert(points_predict.shape == (2, pattern_size[0] * pattern_size[1] * image_count))
delta = points_predict - grids.reshape(pattern_size[0] * pattern_size[1] * image_count, 2).T
assert(delta.shape == (2, pattern_size[0] * pattern_size[1] * image_count))
error = np.mean(np.sum(delta ** 2, axis=0))
print('平均误差:', np.sqrt(error))
# 更新内外参
mat_a = np.matmul(jac.T, jac)
step = -np.matmul(np.mat(mat_a + lamb * mat_i).I,
np.matmul(jac.T, delta.reshape(pattern_size[0] * pattern_size[1] * image_count * 2, 1)))
assert(step.size == 5 + 6 * outer_params.shape[0])
step = np.array(step).flatten()
cx, cy, sx, f, kappa = np.array([cx, cy, sx, f, kappa]) + step[:5]
outer_params += step[5:].reshape(outer_params.shape[0], 6)
# 更新LM算法的参数
points_predict2, _ = predict1(grid_world, cx, cy, sx, sy, f, kappa, outer_params)
delta2 = points_predict2 - grids.reshape(pattern_size[0] * pattern_size[1] * image_count, 2).T
error2 = np.mean(np.sum(delta2 ** 2, axis=0))
points_predict3 = points_predict + np.matmul(jac, step.reshape(5 + 6 * image_count, 1)) \
.reshape(2, pattern_size[0] * pattern_size[0] * image_count)
delta3 = points_predict3 - grids.reshape(pattern_size[0] * pattern_size[1] * image_count, 2).T
error3 = np.mean(np.sum(delta3 ** 2, axis=0))
p = (error - error2) / (error - error3)
lamb = g2 * lamb if p < i1 else \
lamb if i1 <= p < i2 else\
g1 * lamb
print(
'''用LM法优化得到:
cx: %f px;
cy: %f px;
sx: %f um;
sy: %f um;
f: %f mm;
kappa: %f 1/m^2;
''' % (cx, cy, sx * 1e3, sy * 1e3, f, kappa * 1e6)
)
def main():
# 初始参数
# 实际距离全部以毫米为单位
params = {
'pattern size': (7, 7), # 标记圆的个数
'cell width': 25, # 标记点间距
'sx': 4.8e-3,
"sy": 4.8e-3
}
pattern_size = params['pattern size']
# 列出文件夹下的所有图片
directory = './test_images_1'
files = []
import sys
import os
for file in os.listdir(directory):
path = os.path.join(directory, file)
if os.path.isfile(path) and path.endswith('.bmp'):
files.append(path)
if len(files) < 2:
print("至少需要两份标定文件!", sys.stderr)
# exit(128)
# 读取图片
imgs = []
for file in files:
imgs.append(cv.imread(file, cv.IMREAD_GRAYSCALE))
# 检测圆点
grids = np.zeros((len(imgs), params['pattern size'][0] * params['pattern size'][1], 2))
# 有兩種方法可以讀取坐標:
# 1. 直接從halcon的識別結果中讀取坐標(halcon的檢測結果更準);
# 2. 或者調用opencv的檢測算法讀取坐標。
# 注釋掉你不用的那個方法。
'''
# 直接取halcon识别结果
for i, file in enumerate(files):
with open(file + '.d', 'r') as file_halcon_result:
lines = file_halcon_result.readlines()
for j, line in enumerate(lines):
coord = line.strip().split(' ')
if len(coord) != 2:
continue
grids[i, j, 0] = float(coord[0])
grids[i, j, 1] = float(coord[1])
'''
# 从图片提取圆点
for i, img in enumerate(imgs):
success, centers = cv.findCirclesGrid(img, pattern_size)
if not success:
return {
'success': False,
'msg': '标定板无法识别',
'error code 1': 123,
'error code 2': i
}
assert(centers.shape == (pattern_size[0] * pattern_size[1], 1, 2))
grids[i, :, :] = centers.reshape(pattern_size[0] * pattern_size[1], 2)
calibrate(grids, params)
if __name__ == '__main__':
main()7.2 版權信息
圖像: